3

When attempting to recreate and generalise the MatLab code for Random Vectors with Fixed Sum by first principles I came across a few issue with RandomPoint.

According to RandomPoint's documentation it should evaluate on any region that is RegionQ and ConstantRegionQ. However this is not always the case.

For s = 1.2; n = 3;

rng = RegionIntersection[
       Cuboid[ConstantArray[0, n]], 
       Hyperplane[ConstantArray[1, n], s/ConstantArray[n, n]]
      ];

Through@{RegionQ, ConstantRegionQ}@rng

{True, True}

However, 

RandomPoint[rng, 1]

returns unevaluated.

Also, for higher dimensions such as n = 4;

rng4 = RegionIntersection[
       Cuboid[ConstantArray[0, n]], 
       Hyperplane[ConstantArray[1, n], s/ConstantArray[n, n]]
      ];

Through@{RegionQ, ConstantRegionQ}@rng4

{True, True}

but

RandomPoint[rng4, 1]

returning unevaluated.

The n = 3 case can be solved by DiscretizeRegion on rng in RandomPoint.

SeedRandom[123];

RandomPoint[DiscretizeRegion@rng, 1]

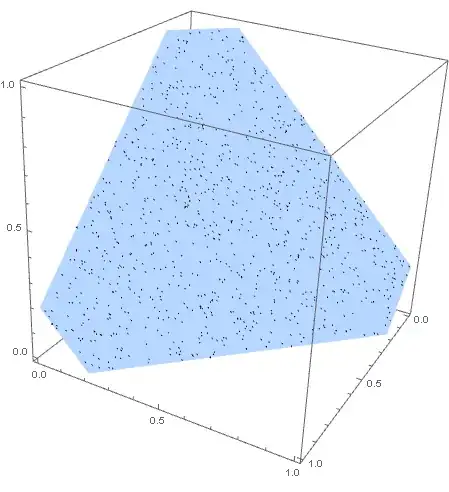
Show[
 Region[rng, Boxed -> True, Axes -> True],
 Graphics3D[{
   Black,
   PointSize@Small,
   Point@RandomPoint[DiscretizeRegion@rng, 1000]
   }]
 ]

{{0.716182,0.258674,0.225143}}

Mathematica graphics

Unfortunately DiscretizeRegion does not work on higher dimensions.

I know that I can generate the vectors in higher dimensions with 

s Standardize[RandomReal[1,n],0&,Total]

but the point is to demonstrate from first principles. That actually doesn't work.

  1. Is there a way to get the expected functionality out of RandomPoint for regions that are RegionQ and ConstantRegionQ?

  2. Can anyone reproduce the issues above? Win 8.1 Mma 11.3.0

Edmund
  • 42,267
  • 3
  • 51
  • 143
  • The algorithm used for rgn4 would generate a random point in the bounded Cuboid and keep those that lie on the unbounded Hyperplane, which would never be expected to happen; so in fact, RandomPoint fails when the dimension of the unbounded region is less than the bounded one. It seems to be an undocumented restriction. – Michael E2 May 20 '18 at 14:20
  • @MichaelE2 Is this not a limitation of RegionIntersection then since it is not producing a bounded region in this case? Should it not produce an $\mathbb{R}^{4}$ polygon in the n=4 case as it does in the n=3 case? Perhaps too complicated so goes for BooleanRegion. – Edmund May 20 '18 at 14:43
  • It's a limitation of RandomPoint, and the restriction applies to rng, too. Yes, the region represents a polyhedron in ${\bf R}^4$. But how would represent that in M except by a union of Simplex[] objects or an intersection of a bounded and unbounded region? If the region is a MeshRegion (which is a union of simplices), then a different algorithm is used, perhaps @ybeltukov's here, which predates RandomPoint. If you can triangulate rng4 into simplices, then RandomPoint will work. – Michael E2 May 20 '18 at 15:00

0 Answers0