There are already good answers, but I'm going to improve the performance, generalize to any region in any dimensions and make the function more convenient. The main idea is to use DirichletDistribution (the uniform distribution on a simplex, e.g. triangle or tetrahedron). This idea was implemented by PlatoManiac and me in the related question obtaining random element of a set given by multiple inequalities (there is also Metropolis algorithm, but it is not suitable here).
The code is relatively short:
RegionDistribution /:
Random`DistributionVector[RegionDistribution[reg_MeshRegion], n_Integer, prec_?Positive] :=
Module[{d = RegionDimension@reg, cells, measures, s, m},
cells = Developer`ToPackedArray@MeshPrimitives[reg, d][[All, 1]];
s = RandomVariate[DirichletDistribution@ConstantArray[1, d + 1], n];
measures = PropertyValue[{reg, d}, MeshCellMeasure];
m = RandomVariate[#, n] &@EmpiricalDistribution[measures -> Range@Length@cells];
#[[All, 1]] (1 - Total[s, {2}]) + Total[#[[All, 2 ;;]] s, {2}] &@
cells[[m]]]
Examples
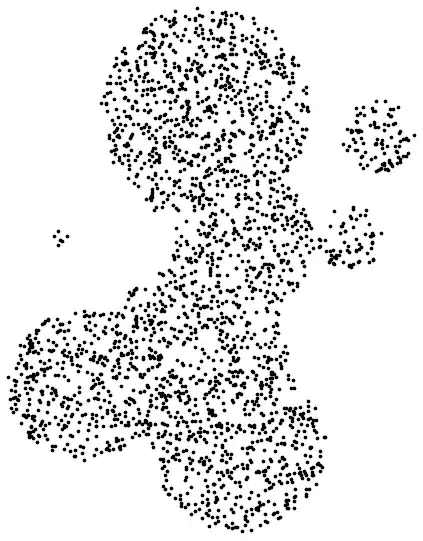
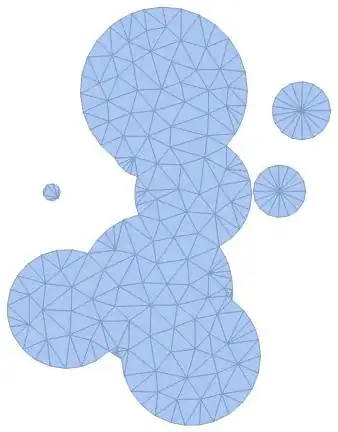
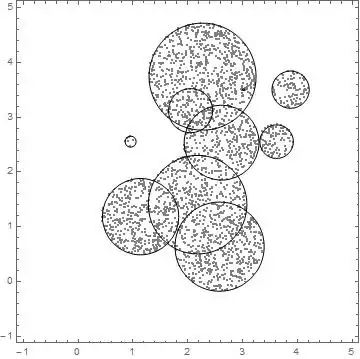
Random disks (2D in 2D)
SeedRandom[0];
region = DiscretizeRegion@RegionUnion@Table[Disk[RandomReal[4, {2}], RandomReal[1]], {10}];
pts = RandomVariate[RegionDistribution[region], 10000]; // AbsoluteTiming
ListPlot[pts, AspectRatio -> Automatic]
{0.004473, Null}
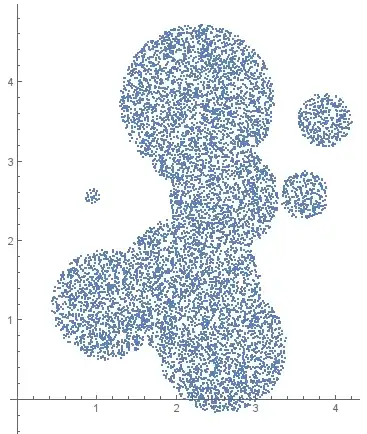
Precise test
pts = RandomVariate[RegionDistribution[region], 200000000]; // AbsoluteTiming
{85.835022, Null}
Histogram3D[pts, 50, "PDF", BoxRatios -> {Automatic, Automatic, 1.5}]
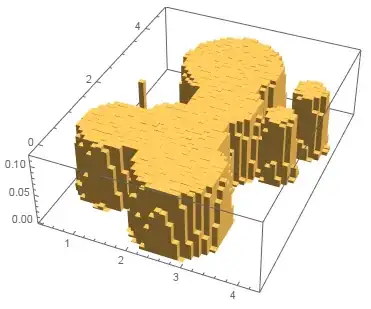
It is fast for $2\cdot10^8$ points and the distribution is really flat!
Intervals (1D in 1D)
region = DiscretizeRegion[Interval[{0, 1}, {2, 4}]];
pts = RandomVariate[RegionDistribution[region], 100000]; // AbsoluteTiming
Histogram[Flatten@pts]
{0.062430, Null}
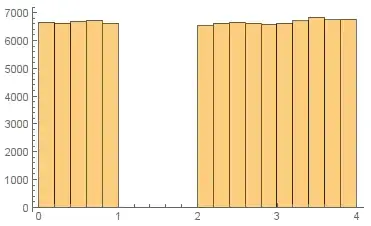
Random circles (1D in 2D)
region = DiscretizeRegion@RegionUnion[Circle /@ RandomReal[10, {100, 2}]];
pts = RandomVariate[RegionDistribution[region], 10000]; // AbsoluteTiming
ListPlot[pts, AspectRatio -> Automatic]
{0.006216, Null}

Balls (3D in 3D)
region = DiscretizeRegion@RegionUnion[Ball[{0, 0, 0}], Ball[{1.5, 0, 0}], Ball[{3, 0, 0}]];
pts = RandomVariate[RegionDistribution[region], 10000]; // AbsoluteTiming
ListPointPlot3D[pts, BoxRatios -> Automatic]
{0.082202, Null}

Surface cow disctribution (2D in 3D)
region = DiscretizeGraphics@ExampleData[{"Geometry3D", "Cow"}];
pts = RandomVariate[RegionDistribution[region], 2000]; // AbsoluteTiming
ListPointPlot3D[pts, BoxRatios -> Automatic]
{0.026357, Null}
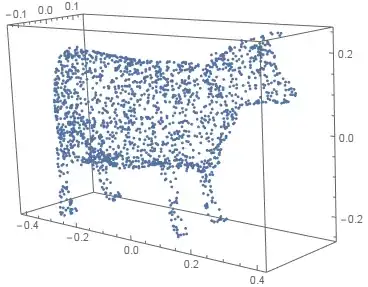
Line in space (1D in 3D)
region = DiscretizeGraphics@ParametricPlot3D[{Sin[2 t], Cos[3 t], Cos[5 t]}, {t, 0, 2 π}];
pts = RandomVariate[RegionDistribution[region], 1000]; // AbsoluteTiming
ListPointPlot3D[pts, BoxRatios -> Automatic]
{0.005056, Null}














FindInstanceis not for generating random numbers ... If you already have the disks, it's trivial to find an instance of a point which lies within them. Take the centre of any disk. It doesn't even matter that you have several disks, you can just use a single one. If you have any expectation that these numbers will be uncorrelated and uniformly distributed (within the disks) then do not useFindInstance. – Szabolcs Aug 22 '14 at 20:09MeshRegions orBoundaryMeshRegions e.g. see here. – RunnyKine Aug 22 '14 at 20:32MeshRegion, try it and see (removeDiscretizeRegion). Its weird, and I'm reporting it. – rcollyer Aug 22 '14 at 20:53regionsatisfiesRegionQfunction but cannot be used just as a "normal" region in other function or structure(ie.Reduce,FindInstance, etc). I think it is a little bug. In the highly coherent system like Mathematica, it should not let this problem happen. And the way fixing this little problem seems pretty easy. – Eric Aug 22 '14 at 21:29region) and @Junho Lee(for giving the solution to workFindInstancewithregion). – Eric Aug 22 '14 at 21:50