I am trying to help this guy here to vizualise the integration volume. How can I plot the different integrals ie a ball and the ball adjusted by a trigonometric function?
Integrals needing visual cue: what does their spanned volume look like?
He was wondering why the first integral is not spherical. I want to provide some sort of visual cue in this kind of issues.
$$\int_0^{2\pi}\int_0^{\pi} d\theta d\phi = 2 \pi^2$$
$$\int_0^{2\pi}\int_0^{\pi} \sin\theta d\theta d\phi = 4 \pi$$
Here's another demonstration (CDF, v9 but works with lower versions) I use in class:
Manipulate[
With[{P0 = ρ (Sin[ϕ] {Cos[θ], Sin[θ], 0} + {0, 0, Cos[ϕ]}),
$θColor = Red, $ϕColor = Darker[Blue], $ρColor = Brown},
Graphics3D[{
{PointSize[Medium], Point[P0],
Line[{{0, 0, 0}, #} & /@ (3 IdentityMatrix[3])], Opacity[0.3],
Line[{{0, 0, 0}, #} & /@ (-3 IdentityMatrix[3])]}, {
{Opacity[0.3],
EdgeForm[Directive[Thickness[Medium], Opacity[0.3]]],
Polygon[{{0, 0, 0}, P0, {P0[[1]], P0[[2]], 0}}], $θColor,
EdgeForm[
Directive[Thickness[Medium],
If[Δρ == 0 && Δϕ == 0 && Δθ == 0, Opacity[1],
Opacity[0.3]], $θColor]],
Polygon[Append[
Table[0.3 {Cos[t], Sin[t], 0}, {t,
Append[Range[0, θ, 0.05], θ]}], {0, 0,
0}]], $ϕColor,
EdgeForm[
Directive[Thickness[Medium],
If[Δρ == 0 && Δϕ == 0 && Δθ == 0,
Opacity[1], Opacity[0.3]], $ϕColor]],
Polygon[Append[
Table[0.5 (Sin[t] {Cos[θ], Sin[θ], 0} + {0, 0,
Cos[t]}), {t,
Append[Range[0, ϕ, 0.05], ϕ]}], {0, 0, 0}]]},
Line[{{P0, {0, 0, P0[[3]]}}, {{P0[[1]], P0[[2]], 0}, {P0[[1]], 0,
0}}, {{P0[[1]], P0[[2]], 0}, {0, P0[[2]], 0}}}],
Point[DiagonalMatrix[P0]]
},
Which[
Δρ == 0 && Δϕ == 0 && Δθ == 0,
{ Thick, $ρColor, Line[{{0, 0, 0}, P0}] },
Δρ == 0 && Δϕ == 0(*&&Δθ>0*), {
First@
ParametricPlot3D[ρ (Sin[ϕ] {Cos[t], Sin[t], 0} + {0,
0, Cos[ϕ]}), {t, θ, θ + Δθ},
PlotStyle -> Directive[Thick, $θColor]]
},
Δρ == 0 &&(*Δϕ>
0&&*)Δθ == 0, {
First@
ParametricPlot3D[ρ (Sin[s] {Cos[θ], Sin[θ],
0} + {0, 0,
Cos[s]}), {s, ϕ, ϕ + Δϕ},
PlotStyle -> Directive[Thick, $ϕColor]]
},
(*Δρ>
0&&*)Δϕ == 0 && Δθ == 0, {
First@
ParametricPlot3D[
r (Sin[ϕ] {Cos[θ], Sin[θ], 0} + {0, 0,
Cos[ϕ]}), {r, ρ, ρ + Δρ}, PlotStyle -> Directive[Thick, $ρColor]]
},
Δρ == 0(*&&Δϕ>
0&&Δθ>0*), {
First@
ParametricPlot3D[ρ (Sin[s] {Cos[t], Sin[t], 0} + {0, 0, Cos[s]}),
{s, ϕ, ϕ + Δϕ},
{t, θ, θ + Δθ}, Mesh -> None,
PlotStyle -> Directive[Lighter[$ρColor]]]
},
(*Δρ>0&&Δϕ>
0&&*)Δθ == 0, {
First@
ParametricPlot3D[ r (Sin[s] {Cos[θ], Sin[θ], 0} + {0, 0, Cos[s]}),
{s, ϕ, ϕ + Δϕ},
{r, ρ, ρ + Δρ}, Mesh -> None,
PlotStyle -> Lighter[$θColor]]
},
(*Δρ>
0&&*)Δϕ == 0(*&&Δθ>
0*), {
First@
ParametricPlot3D[
r (Sin[ϕ] {Cos[t], Sin[t], 0} + {0, 0, Cos[ϕ]}),
{r, ρ, ρ + Δρ},
{t, θ, θ + Δθ},
Mesh -> None, PlotStyle -> Lighter[$ϕColor]]
},
True(*Δρ>0&&Δϕ>
0&&Δθ>0*), {
First@
ParametricPlot3D[ρ (Sin[s] {Cos[t], Sin[t], 0} + {0, 0, Cos[s]}),
{s, ϕ, ϕ + Δϕ},
{t, θ, θ + Δθ}, Mesh -> None,
PlotStyle ->
Dynamic@Directive[Lighter[$ρColor], Opacity[opacity]]],
First@
ParametricPlot3D[
r (Sin[s] {Cos[θ], Sin[θ], 0} + {0, 0, Cos[s]}),
{s, ϕ, ϕ + Δϕ},
{r, ρ, ρ + Δρ}, Mesh -> None,
PlotStyle ->
Dynamic@Directive[Lighter[$θColor],
Opacity[opacity]]],
First@ParametricPlot3D[
r (Sin[ϕ] {Cos[t], Sin[t], 0} + {0, 0, Cos[ϕ]}),
{r, ρ, ρ + Δρ},
{t, θ, θ + Δθ}, Mesh -> None,
PlotStyle ->
Dynamic@Directive[Lighter[$ϕColor], Opacity[opacity]]],
First@ParametricPlot3D[(ρ + Δρ) (Sin[s] {Cos[t], Sin[t], 0} + {0, 0, Cos[s]}),
{s, ϕ, ϕ + Δϕ},
{t, θ, θ + Δθ}, Mesh -> None,
PlotStyle ->
Dynamic@Directive[Lighter[$ρColor], Opacity[opacity]]],
First@ParametricPlot3D[
r (Sin[s] {Cos[θ + Δθ],
Sin[θ + Δθ], 0} + {0, 0, Cos[s]}),
{s, ϕ, ϕ + Δϕ},
{r, ρ, ρ + Δρ}, Mesh -> None,
PlotStyle ->
Dynamic@Directive[Lighter[$θColor],
Opacity[opacity]]],
First@ParametricPlot3D[
r (Sin[ϕ + Δϕ] {Cos[t], Sin[t], 0} + {0, 0, Cos[ϕ + Δϕ]}),
{r, ρ, ρ + Δρ},
{t, θ, θ + Δθ}, Mesh -> None,
PlotStyle ->
Dynamic@Directive[Lighter[$ϕColor], Opacity[opacity]]]
}
]
},
SphericalRegion -> True, PlotRange -> 2, Lighting -> "Neutral"
]],
Row[{Control[{{ρ, 1}, 0, 2, ImageSize -> Small}],
Control[{Δρ, 0, 1, ImageSize -> Small}]},
Spacer[1]],
Row[{Control[{ϕ, 0, π, ImageSize -> Small}],
Control[{Δϕ, 0, π, ImageSize -> Small}]},
Spacer[1]],
Row[{Control[{θ, 0, 2 π, ImageSize -> Small}],
Control[{Δθ, 0, 2 π,
ImageSize -> Small}]}, Spacer[1]],
{{opacity, 1}, 0, 1}, ControlPlacement -> Left
]
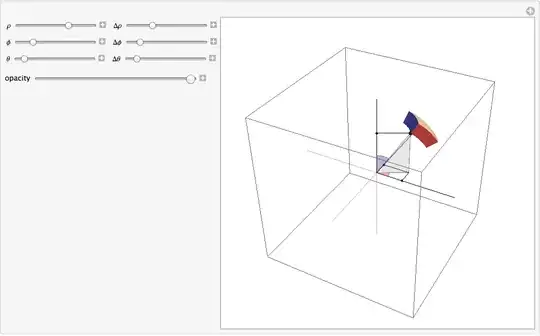
I might add that the reason for submitting it was that it shows, if one moves the ϕ slider, that the surface area element $dS$ or volume element $dV$ decreases as ϕ moves toward 0, or $\pi$, which is in part what his question was about.
ParametricPlot3D::nlnum and Visualization`Core`ParametricPlot3D::invfuncs errors when using it. It happens when all three Δ* values are set. Here's a case when this happens: {opacity = 1, Δθ = 1, Δρ = 1, Δφ = 1, θ = 0, ρ = 1, φ = 0}. I haven't looked through the code to see where or why this occurs, but it'll be quicker for you to find it
– rm -rf
Jan 08 '13 at 22:31
buildVolume that way both the graphics generation is easier to read, and the whole special case handling.
– jVincent
Jan 09 '13 at 00:32
buildVolume can be localized. The students don't see the code, only the output. It's for a calculus class. I was trying to help the OP with the last line in his question. I didn't mean it to be an example program (sorry if that's bad form), but I did mean that it should work! It wasn't until I suspected the pasted code was corrupted that I could fix my answer.
– Michael E2
Jan 09 '13 at 01:06
Here's a very basic demonstration:
Manipulate[
ParametricPlot3D[{Sin[theta] Cos[phi],
Sin[theta] Sin[phi], Cos[theta]},
{theta, 0, t}, {phi, 0, p},
PlotRange -> {{-1, 1}, {-1, 1}, {-1, 1}}],
{t, 0.1, Pi}, {p, 0.1, 2 Pi}]
SphericalPlot3D? – whuber Jan 08 '13 at 18:51Graphics3D[Sphere[]]. Are you wishing to parametrize the surface with spherical coordinates? – Michael E2 Jan 08 '13 at 18:52