I am trying to calculate the change of the refractive index from the change of the absorption coefficient using the Kramers-Kronig relations, in Mathematica.
c = 300000000;
daF[l_] = 500 * 0.28 Exp[-((l - 500)/90)^2];
dnFpoints = Table[
{
ln,
c/Pi NIntegrate[
daF[li] / ((2 Pi c 10^9 /li)^2 - (2 Pi c 10^9 / ln)^2),
{li, 800, 200},
Method -> {"PrincipalValue"},
Exclusions -> ((2 Pi c 10^9 /li)^2 - (2 Pi c 10^9 / ln)^2) == 0
]
},
{ln, 300, 600}
];
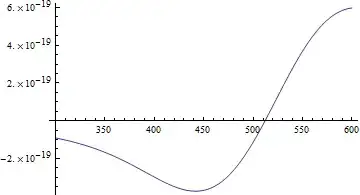
Unfortunately, Mathematica displays an error that it does not converge to prescribed accuracy and the output is junk (I would expect a smooth curve with a negative minimum first and then a positive maximum). I am using version 8, if it matters. Any ideas?

lnforliwhat islnthen? I couldn't find a definition for it in the above code and get a non-numerical values error. – Matariki Feb 14 '12 at 18:43daF[li]/(f1(li)-f2(ln))overlifrom200to800, and then collects results inTable[{ln, integral(ln)}, {ln, 300, 600}]. Therefore we can't change variablesliandln. – Artes Feb 14 '12 at 18:57Method -> "PrincipalValue", Exclusions -> somethingfor certain kinds of functions. It is just a kind of issue when working with numerics, and do not think it is a bug since you get messages. – Artes Feb 16 '12 at 21:0610^9in the integrand so I think this is the reason of appearing different orders of magnitude. – Artes Feb 16 '12 at 21:06