I know that:
$$\int\limits_0^\infty \left(\sqrt{x}-\sqrt{\sqrt{1+x^2}-1}\,\right)\sin{x}\,\text{d}x = \frac{1}{2}\,\sqrt{\frac{\pi}{2}}\,\frac{e-1}{e}$$
but
Integrate[(Sqrt[x] - Sqrt[Sqrt[1 + x^2] - 1]) Sin[x], {x, 0, Infinity}]
yields the integral itself in output after a few seconds.
Is there a way to get the correct result or can MMA provide only an approximation?
I found a way to fool MMA, that is to expand the double radical:
Integrate[(Sqrt[x] - Sqrt[(-1 + I x)/2] - Sqrt[(-1 - I x)/2]) Sin[x], {x, 0, Infinity}]
((-1 + E) Sqrt[\[Pi]/2])/(2 E)
Is there a command that does this automatically?
Deepening further, I noticed that by writing:
Plot[Sqrt[Sqrt[1 + x^2] - 1] - (Sqrt[(-1 + I x)/2] + Sqrt[(-1 - I x)/2]), {x, -10, 10}]
we get:
and this, if I am not mistaken, indicates that MMA does not have an algorithm that can establish its equivalence.

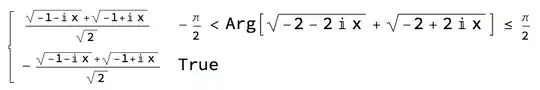
NIntegrate. – JungHwan Min Jul 12 '18 at 17:42NIntegratecode:Sqrt[Pi/2]/2*((E - 1)/E) - NIntegrate[(Sqrt[x] - Sqrt[Sqrt[1 + x^2] - 1])*Sin[x], {x, 0, Infinity}, WorkingPrecision -> 200]almost zero. – Mariusz Iwaniuk Jul 12 '18 at 18:56-Cos[1] + Sqrt[Pi/2] FresnelC[Sqrt[2/Pi]] + Sum[((-1)^(1 + n) (-1 + n) Sqrt[2/Pi] Gamma[-(7/2) + 2 n] HypergeometricPFQ[{-(1/2) + n}, {3/2, 1/2 + n}, -(1/4)])/Gamma[2 n] - ((1/16 + I/16) I^n (-I + (-1)^n) (Gamma[5/4 - n/2] Gamma[-(1/2) + n] HypergeometricPFQRegularized[{5/4 - n/2}, {3/2, 9/4 - n/2}, -(1/4)] + 4 Sqrt[Pi] Sec[n Pi] Sin[1/4 (Pi + 2 n Pi)]))/Gamma[1 + n], {n, 1, Infinity}]. – AccidentalFourierTransform Jul 12 '18 at 20:35Integrate[ Sin[x]/(2 Sqrt[x] ), {x, 0, Infinity} ](*Sqrt[\[Pi]/2]/2*)– Ulrich Neumann Jul 13 '18 at 06:14