Drawing the Pursuit curves

Question

I was reading this post on Filling Space with Pursuit Polygons. I didn't really see where the filling was, but found it quite interesting.

Then I saw these pursuit curves.

They seem to have used a different logarithm. For example looking at the square, by tweaking the code from the previous code, I got this

With[{data = {{0, 0}, {1, 0}, {1, 1}, {0, 1}, {0, 0}}},  Graphics[{Table[{Scale[       Rotate[Line[data], 90/11*x Degree], {x, x}]}, {x, 0, 11}]}]]

Both picture has 11 sets of squares. With a bit trial and error, I got as close as possible by changing the angles.

How can I get the identical pictures?

And these ones below, which looks more challenging.

related: Is it possible to draw this figure using Mathematica?. — AccidentalFourierTransform, Jul 12 '18 at 21:42
@AccidentalFourierTransform Aha, so satifying to look at and what a temptation to try this! I don't think pursuit curve is the only thing I will be pursuing now! Thanks. — Chen Stats Yu, Jul 12 '18 at 21:51
I don't quite get the difference between this and the Q&A you linked. The figures in both seem similar and have a similar variety. Is it just that you want to reproduce these specific images? — Michael E2, Jul 12 '18 at 22:40
@MichaelE2 Yes and no. Sorry about the confusion. I was looking at the Pursuit curves and then I found the images above. Now I realised from the answers posted, the images are not exactly pursuit curves if I understood it correctly. Being able to produce any images of such type is quite satisfying. — Chen Stats Yu, Jul 12 '18 at 22:44

halirutan · Answer 1 · 2018-07-12T21:55:59.563

I have made a very detailed post about these patterns on my website

A simple scheme for a line-pattern

I won't repeat everything I have written there, but I explained in detail how this can be done in Mathematica and gave the full source code.

Edit

If you are wondering how to recreate the figure that you think is beautiful, please look at it carefully and try to find the underlying triangles that divide the large triangle.

You will see that you have a hexagon made of triangles in the center and on each second side you have one triangle outwards. The hardest part is to create these 10 triangles and (as I say in my blogpost) make them have the right direction (the order of the 3 points of each triangle).

There is surely an easier way to do this, but this hack will do to create the initial triangle points. It uses the points for a hexagon and creates all necessary triangles at once, taking care of their rotation:

pts = Table[{Cos[phi], Sin[phi]}, {phi, 0, 2 Pi, 2/6 Pi}];
tris = Flatten@MapIndexed[
    With[{odd = OddQ[#2[[1]]]},
      {triangle @@ Prepend[
         If[odd, Reverse, Identity]@#, {0, 0}],
       If[Not[odd],
        triangle[
         Plus @@ #, #[[1]], #[[2]]
         ],
        {}
        ]
       }
      ] &, Partition[pts, 2, 1]];

The rest is copying the code. As you might note, I have wrapped all triangle points into a triangle head. Now, we simply create the inner lines by replacing them and using the function from the site:

calcPoints[pts : {pcurr_, pnext1_, pnext2_, rest___}, f_, result_] := 
  calcPoints[{pnext1 + f*(pnext2 - pnext1), pnext2, rest, pcurr}, 
    f, {result, pcurr}] /; isNotTooShort[pts];

calcPoints[pts_, _, result_] := Partition[Flatten[result], 2];

isNotTooShort[pts_] := 
  Total[SquaredEuclideanDistance @@@ Partition[pts, 2, 1]] > 0.05

Graphics[{Thickness[.003], Darker[Gray], 
  tris /. triangle[pts__] :> {Line[calcPoints[{pts}, .12, {}]], 
     Line[Append[{pts}, First[{pts}]]]}}]

Mathematica graphics

Never came cross my mind the search for “line pattern”. Thanks. I will take a look! — Chen Stats Yu, Jul 12 '18 at 20:38
That's completely my fault. I guess I didn't want a difficult title and decided to simply call it line patterns. — halirutan, Jul 12 '18 at 20:56
Hahahah maybe just “add” the proper fancy name to it too — Chen Stats Yu, Jul 12 '18 at 21:04

AccidentalFourierTransform · Accepted Answer · 2018-07-12T22:29:32.077

In this answer of mine I wrote a simple function that will draw the curve you are after, given an arbitrary polygon:

g[x_] := Fold[Append[#1, BSplineFunction[#1[[#2]], SplineDegree -> 1][.1]] &, x, Partition[Range[200], 2, 1]]

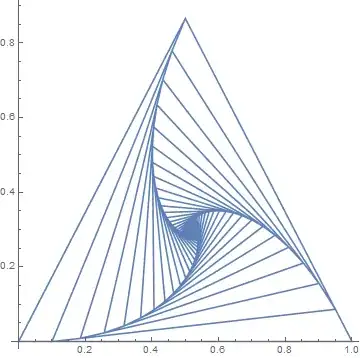
For example, given the triangle

ListPlot[Prepend[{{0, 0}, {1, 0}, {1/2, Sqrt[3]/2}}, {1/2, Sqrt[3]/2}], AspectRatio -> 1, Joined -> True, PlotRange -> All]

we get

ListPlot[Prepend[g@{{0, 0}, {1, 0}, {1/2, Sqrt[3]/2}}, {1/2, Sqrt[3]/2}], AspectRatio -> 1, Joined -> True, PlotRange -> All]

With this, it is just a matter of combining triangles to generate all the figures in the OP.

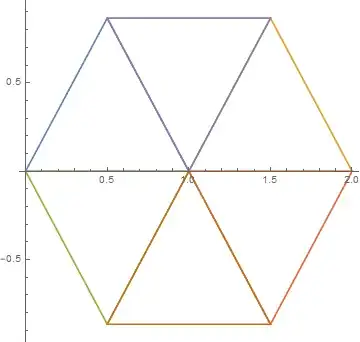
For example, given the hexagon

ListPlot[{Prepend[{{0, 0}, {1, 0}, {1/2, Sqrt[3]/2}}, {1/2, Sqrt[3]/2}], Prepend[{{1, 0}, {2, 0}, {3/2, Sqrt[3]/2}}, {3/2, Sqrt[3]/2}], Prepend[{{0, 0}, {1, 0}, {1/2, -(Sqrt[3]/2)}}, {1/2, -(Sqrt[3]/2)}], Prepend[{{1, 0}, {2, 0}, {3/2, -(Sqrt[3]/2)}}, {3/2, -(Sqrt[3]/2)}], Prepend[{{1/2, Sqrt[3]/2}, {3/2, Sqrt[3]/2}, {1, 0}}, {1, 0}], Prepend[{{1/2, -(Sqrt[3]/2)}, {3/2, -(Sqrt[3]/2)}, {1, 0}}, {1, 0}]}, AspectRatio -> 1, Joined -> True, PlotRange -> All]

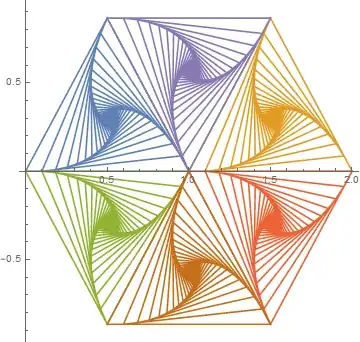
we get

ListPlot[{Prepend[g@{{0, 0}, {1, 0}, {1/2, Sqrt[3]/2}}, {1/2, Sqrt[3]/2}], Prepend[g@{{1, 0}, {2, 0}, {3/2, Sqrt[3]/2}}, {3/2, Sqrt[3]/2}], Prepend[g@{{0, 0}, {1, 0}, {1/2, -(Sqrt[3]/2)}}, {1/2, -(Sqrt[3]/2)}], Prepend[g@{{1, 0}, {2, 0}, {3/2, -(Sqrt[3]/2)}}, {3/2, -(Sqrt[3]/2)}], Prepend[g@{{1/2, Sqrt[3]/2}, {3/2, Sqrt[3]/2}, {1, 0}}, {1, 0}], Prepend[g@{{1/2, -(Sqrt[3]/2)}, {3/2, -(Sqrt[3]/2)}, {1, 0}}, {1, 0}]}, AspectRatio -> 1, Joined -> True, PlotRange -> All]

Tweaking the parameters and using black lines, we get

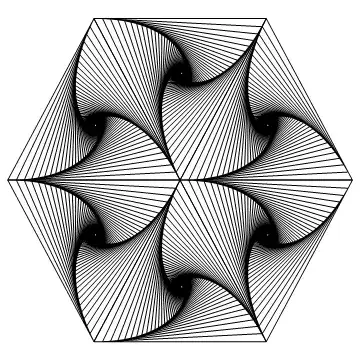
which is almost identical to the figure in the OP. Similarly,

while the rest of figures are left to the reader.

I don't think it's quite the same as the square I was looking at. It was just a simple rotation with a corresponding scale factor. In your graph, one of the vertices stays. Am I right? — Chen Stats Yu, Jul 12 '18 at 22:07
I think my title was misleading now. The square I was looking at is NOT a pursuit curve... — Chen Stats Yu, Jul 12 '18 at 22:09

Chen Stats Yu · Answer 3 · 2018-07-12T22:14:03.273

I did a very crude trial and experiment by choosing an angle, then working out the scale factor so that the squares stay touch.

Graphics@With[{data = {{0, 0}, {1, 0}, {1, 1}, {0, 1}, {0, 0}}},   Table[Scale[     Rotate[Line[data],  30*n Degree], {0.7320508075688773^n,      0.7320508075688773^n}], {n, 0, 11}]]

Result is pretty satisfying given where I started.

Updates

Again, very crude attempt:

mydraw[repeat_: 3, angle_: 30] := Module[
    {data, x, y, scale},
    data = {{0, 0}, {1, 0}, {1, 1}, {0, 1}, {0, 0}};
    scale = Sqrt[x^2 + y^2] /. NSolve[{x + y == 1, Tan[angle Degree] == x/y}, {x, y}, Reals][[1]];
    Graphics@Table[Scale[Rotate[Line[data], angle*n Degree], {scale^n, scale^n}], {n, 0, repeat}]
];
mydraw[]

It works for the purpose:

Drawing the Pursuit curves

3 Answers3

Edit

Linked