How to plot planar graphs as such?

Question

A planar graph is a graph that can be drawn in the plane such that no two edges cross.

For example, the graph Graph[{{1, 2}, {2, 3}, {3, 1}, {1, 4}, {3, 4}, {2, 4}}] is planar, and can be shown in both of these ways:

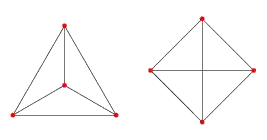
enter image description here

The layout in the left doesn't have crossing edges and it's immediately obvious that the graph is planar. The layout on the right is what Mathematica gives me by default.

Question: How can a planar graph be shown without any crossing edges in Mathematica?

I expect Combinatorica` might have this feature as it has a PlanarQ function, but unfortunately the documentation is not included with Mathematica and I have not been able to find out how to do this.

Testing whether a Graph is planar is possible like this:

<< GraphUtilities`
PlanarQ@ToCombinatoricaGraph[someGraph]

Note: The above way of testing planarity is for version 8 or earlier. The PlanarGraphQ built-in function was introduced in version 9.

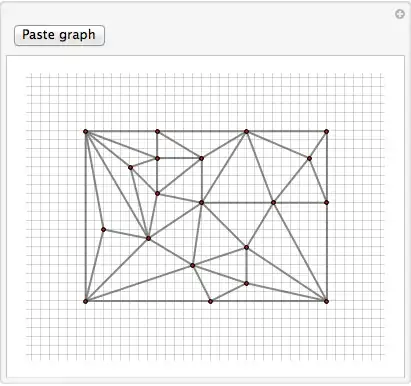
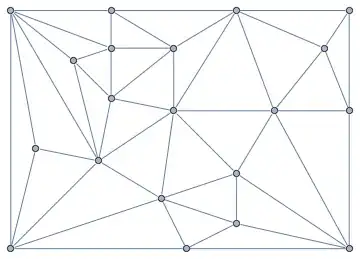
Here's a random set of planar graph of different sizes to test on:

<< ComputationalGeometry`
graphs = DeleteDuplicates[
   Flatten@Table[
     Graph@
      Union[Sort /@ 
        Join @@ (Thread /@ 
           DelaunayTriangulation@RandomReal[1, {j, 2}])],
     {10}, {j, 4, 10}
     ], IsomorphicGraphQ];

To avoid confusion, I'd like to note that the ComputationalGeometry`PlanarGraphPlot[] function does not do what I need. It does not lay out a graph. One needs to provide an explicit list of vertex coordinates to it. I have a graph as the input, I know that it's planar, and need a layout algorithm that will draw the graph without intersecting edges.

What do you mean: the documentation is not included with Mathematica? — Mr.Wizard, Feb 15 '12 at 14:35
@Mr.Wizard The full documentation of Combinatorica` is not included. It has to be bought separately. — Szabolcs, Feb 15 '12 at 14:47
Did you try selecting RadialDrawing in the right-click context menu under Graph Layout. For this example it gives the graph on the left. — kglr, Feb 15 '12 at 14:48
On the other hand, GraphData["TetrahedralGraph"] is drawn such that it is obviously planar... — J. M.'s missing motivation, Feb 15 '12 at 14:53
@kguler I tried that and other options... it gives the correct plot for the first example and for a few in the second bigger list of graphs, but not all... — rm -rf, Feb 15 '12 at 15:02
GraphData["Classes"] returns 163 classes of which oneis "Planar" and GraphData["Planar"] returns 2923 graphs. Perhaps, this list could serve as some sort of look-up table? — kglr, Feb 15 '12 at 15:14
This paper, posted by @halirutan in chat, seems to suggest this is not a trivial thing to do: http://www.math.uni-hamburg.de/home/schacht/2011/untangle.pdf — Szabolcs, Feb 15 '12 at 15:37
@kguler Even the graphs returned by GraphData don't contain vertex position information, so it doesn't solve the visualization problem. Testing planarity is not a problem, PlanarQ does that. Also, lookup tables with graphs are really problematic because they require a lot of isomorphism testing (which can be slow---and version 8.0.4 IsomorphicGraphQ is still buggy unfortunately) — Szabolcs, Feb 15 '12 at 15:43
Have a look at Help > Documentation Center > ComputationalGeometry/ref/PlanarGraphPlot — Daniel Lichtblau, Feb 15 '12 at 17:14
@Daniel I found that function, but it requires a set of points (coordinate pairs) as input and it simply shows a Delaunay triangulation of these points. It does not seem to take a graph as input without explicit point coordinates. I only have the graph (e.g. as an adjacency list), I can test using PlanarQ that it is indeed a planar graph, and now I would like to show it as a planar graph (i.e. without intersecting edges) — Szabolcs, Feb 15 '12 at 17:44
MathGroup version here: https://groups.google.com/d/topic/comp.soft-sys.math.mathematica/_lxnrJ0fufc/discussion — Szabolcs, Feb 16 '12 at 10:42

Sjoerd C. de Vries · Accepted Answer · 2013-01-28T06:15:35.540

19

You can plot it using the GraphLayout option, which has, since v9, "PlanarEmbedding" as a possible value:

Graph[Rule @@@ {{1, 2}, {2, 3}, {3, 1}, {1, 4}, {3, 4}, {2, 4}}, GraphLayout -> "PlanarEmbedding"]

Mathematica graphics .

(BTW: This is the standard Mathematica Graph, not the Combinatorica Graph function)

Another one:

truncatedCube =
  {{0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1}, {1, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1}, 
   {1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1}, {1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0}, 
   {0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0}, {1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0}, 
   {0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0}, {1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0}, 
   {0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, 
   {0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0}, {1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0}, 
   {0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}};

AdjacencyGraph[truncatedCube, 
  GraphLayout -> "PlanarEmbedding", 
  VertexLabels -> Array[# -> # &, Length @ truncatedCube], 
  PlotRangePadding -> 0.5]

Mathematica graphics

Without GraphLayout -> "PlanarEmbedding":

Mathematica graphics

edited Jan 28 '13 at 06:15

answered Jan 27 '13 at 21:01

Sjoerd C. de Vries

65,815
14
188
323

1

Excellent! I do wonder if this (new in version 9) method is guaranteed to find a planar embedding if one exists. – Szabolcs Jan 28 '13 at 00:08
1

@Szabolcs since v9 there's also PlanarGraphQ. I suppose that mma will try to find the solution if it knows it exists. Anyway, the documentation says nothing about this but I tried quite a few cases. – Sjoerd C. de Vries Jan 28 '13 at 06:19
3

I wrote support and they confirmed (in less than 24 hrs!!) that if the graph is planar, this method should always find a planar embedding (i.e. it's not a heuristic method). I'll mention PlanarGraphQ in the question in case people read it. – Szabolcs Jan 28 '13 at 16:32
@Szabolcs Great! – Sjoerd C. de Vries Jan 28 '13 at 21:47
Is it possible to do this given a graph taken from GraphData? – Juan Jan 26 '16 at 20:13
@Juan Why wouldn't that be the case? GraphData graphs are just graphs. Try for instance Graph[GraphData[{"TriangularHoneycombObtuseKnight", 5}] // EdgeList // Graph, GraphLayout -> "PlanarEmbedding"] – Sjoerd C. de Vries Jan 26 '16 at 20:39
@SjoerdC.deVries I don't know what these // mean, but I tried Graph[EdgeList[GraphData["BislitCube"]], GraphLayout -> "PlanarEmbedding"] and it worked!. Edit: OK I think they are some way to do function composition. This works too: Graph[GraphData["BislitCube"] // EdgeList, GraphLayout -> "PlanarEmbedding"]. – Juan Jan 26 '16 at 20:58
@juan Functions can be entered in Mathematica in a standard format with fun[arg], prefix form as fun@arg, infix as arg1~fun~arg2, and postfix form as arg//fun. Sometimes, one of the forms is more convenient or fits more with your mental image of the program flow. Note that precedence of the various forms differs. – Sjoerd C. de Vries Jan 26 '16 at 21:04

score 17 · Answer 2 · answered Mar 02 '12 at 14:44

17

I wouldn't know how to do this automatically but you could untangle the graphs manually using Manipulate:

untangle[gr_] :=
 DynamicModule[{edges, vv, plrnge, gap},
  gap = .15;
  edges = EdgeList[gr];
  vv = VertexList[gr];
  plrnge = 
   Through[{Min, Max}[#]] & /@ 
    Transpose[
     OptionValue[AbsoluteOptions[gr, VertexCoordinates], 
      VertexCoordinates]];
  Manipulate[
   pt = Round[pt, .15];
   Graph[vv, edges, VertexCoordinates -> pt,
    EdgeStyle -> {{Darker[Gray], Thickness[Large]}},
    VertexSize -> 0,
    GridLines -> (Range[Floor[#1 - 1, gap], #2 + 1, gap] & @@@ plrnge),
    GridLinesStyle -> Opacity[.3],
    PlotRange -> plrnge + {{-1, 1}, {-1, 1}},
    Epilog -> {EdgeForm[Black], FaceForm[Red], 
      Disk[#, .03] & /@ pt}],
   {{pt, OptionValue[AbsoluteOptions[gr, VertexCoordinates],
      VertexCoordinates]}, Locator, Appearance -> None},
   Button["Paste graph", Print[Graph[vv, edges, VertexCoordinates -> pt]]]]]

Example

For some arbitrary test graph this looks like

<< ComputationalGeometry`
graph = Graph@
   Union[Sort /@ 
     Join @@ (Thread /@ DelaunayTriangulation@RandomReal[1, {20, 2}])];
untangle[graph]

Before:

Mathematica graphics

And after manually untangling the vertices:

Mathematica graphics

The pasted untangled graph looks like:

Mathematica graphics

answered Mar 02 '12 at 14:44

Heike

35,858
3
108
157

3

It's not that easy to do the untangling even manually though. – Szabolcs Mar 02 '12 at 14:48
8

No, I know. Maybe you could turn it into a puzzle and let other people do the untangling :-) – Heike Mar 02 '12 at 14:56
4

I could make a web based game, and feed all my graphs to the visitors :D – Szabolcs Mar 02 '12 at 14:59
7

That's how I am usually suckered into solving other people's problems. – Heike Mar 02 '12 at 15:05
4

SE is a big game, isn't it? :D – Szabolcs Mar 02 '12 at 15:06
1

@Szabolcs comments above quoted in my profile. – Mr.Wizard Jan 28 '13 at 01:27
1

@Szabolcs There is already a nice web-based planarity game at http://www.planarity.net – Mike Z. Jan 28 '13 at 03:27
and also an Entangled game for android. – Emilio Pisanty Aug 22 '14 at 07:55

score 4 · Answer 3 · answered Nov 06 '18 at 21:15

There are the built-in "PlanarEmbedding" and "TutteEmbedding" GraphLayouts.

IGraph/M brings additional planar graph visualization functions, IGLayoutPlanar and IGLayoutTutte. IGLayoutPlanar implements a different algorithm than "PlanarEmbedding" and IGLayoutTutte allows specifying the outer face, and considers edge weights (the builtin one can do neither). In addition to IGraph/M's documentation, there are some demos in this post.

How to plot planar graphs as such?

3 Answers3

Linked