Finding face vertices from the face adjacency graph

Question

I have a question about face adjacency graphs.

Suppose that I have an adjacency matrix

M = {{0, 1, 0, 0, 1, 1, 0, 0}, 
     {1, 0, 1, 0, 0, 0, 0, 1},  
     {0, 1, 0, 1, 0, 0, 1, 0}, 
     {0, 0, 1, 0, 1, 0, 1, 0}, 
     {1, 0, 0, 1, 0, 1, 0, 0}, 
     {1, 0, 0, 0, 1, 0, 0, 1}, 
     {0, 0, 1, 1, 0, 0, 0, 1}, 
     {0, 1, 0, 0, 0, 1, 1, 0}}

that is known to be a planar graph. So I use the command GraphPlot[M] and give vertex labeling. The result is

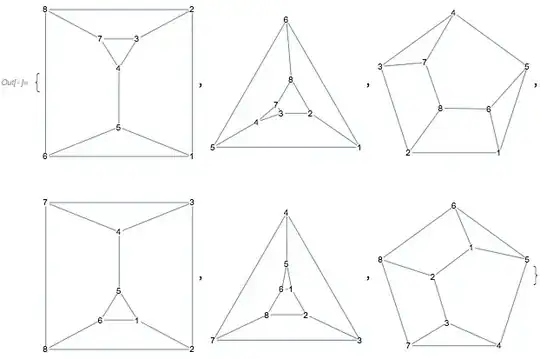
enter image description here

There are 5 faces in the figure (exclude the outer face). The set of vertices of the faces is {{1,6,8,2}, {1,6,5},{4,5,6,8,7},{3,4,7},{2,3,7,8}}.

I don't know how to find this list of vertices automatically if I enter any adjacency matrix (I'm sure that all picked matrices are planar graphs due to PlanarGraph[M])

Are you sure that you are on the right site? This site is dedicated to the program MathematicA, not to MathematicS. — Sjoerd C. de Vries, Jan 26 '13 at 18:55
Do you already have the a layout of the graph (the vertex coordinates for each vertex)? If not, there probably isn't any already implemented simple existing way in Mathematica to lay out the graph without crossing edges. — Szabolcs, Jan 27 '13 at 03:41
The difficulty here is that before you can talk about faces, you need to find an actual embedding of the graph in the plane, without crossing edges. None of Mathematica's built-in layout algorithms will guarantee you this. — Szabolcs, Jan 27 '13 at 04:03
The graph that you show in your question is a vertex connection graph, not a Face Adjacency Graph. The FAG would have this matrix: {{0, 1, 1, 0, 1}, {1, 0, 1, 0, 0}, {1, 1, 0, 1, 1}, {0, 0, 1, 0, 1}, {1, 0, 1, 1, 0}}. Given the title of your question I assume that you want to derive the list of face vertices given the FAG. Correct? — Sjoerd C. de Vries, Jan 27 '13 at 20:27
I don't think there's a built-in command to deal with Face Adjacency Graphs, so this question may be more suited for our sister site math.stackexchange.com. They have at least one [other question](http://math.stackexchange.com/questions/275915/what-kind-of-solid-has-a-face-adjacency-graph-whose-spanning-trees-are-not-feasi on FAGs). You could flag this question for migration using the flag link below the question. — Sjoerd C. de Vries, Jan 27 '13 at 20:33
Anyway, I don't believe it is possible. When mapping faces to a FAG information is lost, just like a projection. Mapping back is not always possible. — Sjoerd C. de Vries, Jan 27 '13 at 20:52
@Szabolcs That's not true. See the answer that I added to the question you linked to. — Sjoerd C. de Vries, Jan 27 '13 at 22:30
@Sjoerd Excellent! This practically solves this question too, see e.g. http://mathoverflow.net/questions/23811/reporting-all-faces-in-a-planar-graph — Szabolcs, Jan 28 '13 at 01:14

score 15 · Answer 1 · edited Apr 23 '18 at 22:05

As Szabolcs mentioned, you could use ordering (PlanarEmbedding) to find faces.

g = AdjacencyGraph[M, GraphLayout -> "PlanarEmbedding", 
             VertexLabels -> "Name", ImagePadding -> 5]

enter image description here

The following function will find next vertex of the face based on the given planar embedding:

nextCandidate[s_, t_, adj_] :=
   Block[{ length, pos},
      length = Length[adj];
      pos = Mod[Position[adj, s][[1, 1]] + 1, length, 1];
      {t, adj[[pos]]}
    ];

The main function to get all faces:

FindFace[g_?PlanarGraphQ] :=
   Block[{emb},
      emb = GraphEmbedding[g, "PlanarEmbedding"];
      FindFace[g, emb]
   ];

FindFace[g_?PlanarGraphQ, emb_] :=
   Block[{m, orderings, pAdj, rightF, s, t, initial, face},
       m = AdjacencyMatrix[g];
       Table[pAdj[v] = 
           SortBy[Pick[VertexList[g], m[[v]], 1], 
           ArcTan @@ (emb[[v]] - emb[[#]]) &], {v, VertexList[g]}];
       rightF[_] := False;
       Reap[
         Table[
           If[! rightF[e],
             s = e[[1]];
             t = e[[2]];
             initial = s;
             face = {s};
             While[t =!= initial,
               rightF[UndirectedEdge[s, t]] = True;
               {s, t} = nextCandidate[s, t, pAdj[t]];
               face = Join[face, {s}];
             ];
             Sow[face];
           ],
         {e, EdgeList[g]}]][[2, 1]]
     ]

For example,

In[162]:= faces = FindFace[g]
Out[162]= {{1, 2, 8, 6}, {1, 5, 4, 3, 2}, {1, 6, 5}, {2, 3, 7, 8}, {3,
     4, 7}, {4, 5, 6, 8, 7}}

coord = GraphEmbedding[g]; 
Graphics[{EdgeForm[Directive[Black, Thick]], 
 Thread[{ColorData[3, "ColorList"][[;; Length[faces]]], 
           Polygon[coord[[#]]] & /@ faces}]}]

enter image description here

You could use the precomputed coordinates if you want like:

g = GridGraph[{3, 3}]

enter image description here

In[166]:= FindFace[g, GraphEmbedding[g]]
Out[166]= {{1, 2, 5, 4}, {1, 4, 7, 8, 9, 6, 3, 2}, {2, 3, 6, 5}, {4, 
     5, 8, 7}, {5, 6, 9, 8}}

Note that this function will find all faces including the external face.

Hope this help you to start this.

"... will find all faces including the external face" Should be easy to filter that out, if the OP chooses to, since it has the max area. Nice answer :) — rm -rf, Jan 29 '13 at 16:03
Your code seem to not work in 10.4 any more.And at this problem I have a same thinking in this post — yode, Apr 08 '16 at 14:14
@yode I just checked on 10.4 and it works fine. What is not working? — halmir, Apr 08 '16 at 16:27
Sorry.In my dormitory pc it work well,but the office not.I'll check it again tomorrow. — yode, Apr 08 '16 at 16:59

score 5 · Answer 2 · edited Apr 13 '17 at 12:56

As Sjoerd noted, version 9 includes a layout algorithm that will avoid edge crossings if the graph is planar. This is the most difficult part of the task, but once you have the planar embedding, it is relatively easy to find the faces.

You can start by finding counterclockwise orderings of vertices around any vertex. Let g be the planar graph, then

emb = GraphEmbedding[g, "PlanarEmbedding"]
m = AdjacencyMatrix[g]

orderings = Table[
  SortBy[
   Pick[VertexList[g], m[[v]], 1],     (* all neigbours of v *)
   ArcTan @@ (emb[[v]] - emb[[#]]) &
  ],
  {v, VertexList[g]}
 ]

Based on this information you can walk the vertices belonging to each face, you just need to make sure you never make a turn greater than 180 degrees.

I don't have time to finish implementing this. I hope this information was helpful and you'll be able to program it.

Jason B. · Answer 3 · 2016-04-11T14:24:50.927

The answer proposed by halmir is very efficient and will give a list featuring all the internal faces along with one face that represents the outer perimeter, but the outer face is not always at the same point in the list, and plotting the polygons sometimes results in obscuring some internal faces.

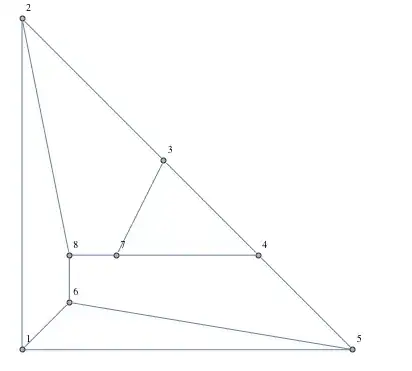
Consider the following graph,

g1 = AdjacencyGraph[{{0, 1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0}, {1, 0, 1, 
    0, 0, 0, 0, 1, 0, 0, 0, 0}, {0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 
    0}, {1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0}, {1, 0, 0, 0, 0, 1, 0, 1,
     0, 0, 0, 0}, {0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0}, {0, 0, 0, 1, 
    0, 1, 0, 0, 0, 0, 0, 1}, {0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0}, {0,
     0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0}, {0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 
    0, 0}, {0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1}, {0, 0, 0, 0, 0, 0, 1,
     0, 0, 0, 1, 0}},
  GraphLayout -> "PlanarEmbedding", 
  VertexCoordinates -> {{0.68, 0.88}, {0.84, 0.85}, {1.12, 
     0.89}, {0.33, 1.13}, {0.81, 0.33}, {0.43, 0.33}, {0.15, 
     1.13}, {0.96, 0.33}, {1.12, 0.33}, {1.12, 1.13}, {-0.12, 
     0.33}, {-0.12, 1.13}}]

The above algorithm will give

faces = FindFace[g1,GraphEmbedding[g1]];
coord = GraphEmbedding[g1];
Graphics[{EdgeForm[Directive[Black, Thick]], 
  Thread[{ColorData[3, "ColorList"][[;; Length[faces]]], 
    Polygon[coord[[#]]] & /@ faces}]}]

which has the polygons in such an order that you can't see all internal faces. The obvious solution (obvious after halmir pointed it out to me) is to remove the element with the largest area. But, as often happens to me, I had spent some time writing a code that does the same thing but much slower (because I didn't think halmir's code worked on the above graph).

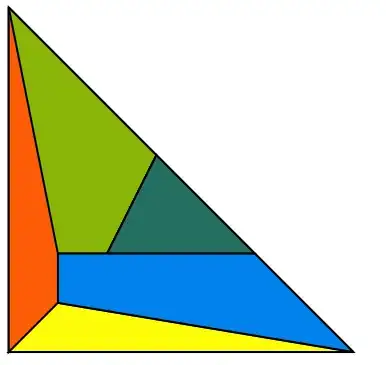
The algorithm I propose should output the list of non-overlapping polygons from the input graph. The idea is to use FindCycles to get a full list of cycles from the graph, then sort this list in terms of the resulting polygon area. We know that the smallest polygon is one we want to keep. Then we look at the rest of the polygons, keeping only those with zero overlap with the current list of faces. This is the slow step, because it uses RegionIntersection to determine whether two polygons overlap.

I use a While loop to make sure that we stop looking at the cycles once we have enough for a complete basis.

graphToFaces[graph_?PlanarGraphQ] := Module[{graphpoints, cycles, polygons, n},
  graphpoints = GraphEmbedding[graph];
  cycles = 
   Polygon[graphpoints[[#]]] & /@ 
    FindCycle[graph,  Max[Length /@ FindFundamentalCycles[graph]], All][[All, All, 2]];
  cycles = SortBy[cycles, Area];
  polygons = {cycles[[1]]};
  n = 2;
  While[Length@polygons < Length@FindFundamentalCycles@graph && 
    n <= Length@cycles,
   If[
    And @@ (Area[Rationalize@cycles[[n]], Rationalize@ #]] === 0 & /@ 
       polygons),
    AppendTo[polygons, cycles[[n]]]
    ];
   n++
   ];
  First /@ (polygons /. 
     Thread[graphpoints -> Range@Length@graphpoints])
  ]

Applied to the problem above,

faces = graphToFaces[g1]
coord = GraphEmbedding[g1];
Graphics[{EdgeForm[Directive[Black, Thick]], 
  Thread[{ColorData[3, "ColorList"][[;; Length[faces]]], 
    Polygon[coord[[#]]] & /@ faces}]}]
(* {{5, 8, 2, 1}, {9, 8, 2, 3}, {2, 3, 10, 4, 1}, {5, 6, 7, 4, 
  1}, {11, 12, 7, 6}} *)

g1 uses predefined coordinates, so to generate corresponding faces you should use the second argument (second example in my answer): FindFace[g1, GraphEmbedding[g1]]. And FindFace generate all faces including outer like I mentioned. Here it's the largest one. To filter out, you can try faces = Most[SortBy[FindFace[g1, GraphEmbedding[g1]], Length]] — halmir, Apr 11 '16 at 13:39
@halmir - now I feel pretty stupid lol :-) I'm new to graphs and computational geometry. — Jason B., Apr 11 '16 at 13:45
@halmir - but it won't always be the largest one by number of vertices, right? It would always be the largest one by Area though, so a foolproof method might be Most[SortBy[FindFace[g1, GraphEmbedding[g1]], Area[Polygon[coord[[#]]]] &]] — Jason B., Apr 11 '16 at 13:54

score 1 · Answer 4 · answered Jun 26 '18 at 11:24

IGraph/M now has functionality to find the faces of a planar graph and to find the dual graph.

g = AdjacencyGraph[M]

IGFaces[g]
(* {{1, 2, 8, 6}, {1, 6, 5}, {1, 5, 4, 3, 2}, {2, 3, 7, 8}, {3, 4, 7}, {4, 5, 6, 8, 7}} *)

This finds all faces, including the outer face. Which face to consider the outer one is arbitrary. It cannot be inferred from the connectivity alone.

Here are six different planar drawings of your graph. The outer face is different in each:

IGLayoutTutte[g, "OuterFace" -> #, VertexShapeFunction -> "Name"] & /@ IGFaces[g]

To find the dual graph, use

dg = IGDualGraph[g]

The vertices of the dual come in the same order as the output of IGFaces. Let's label them:

Graph[dg, VertexLabels -> Thread[VertexList[dg] -> HoldForm /@ IGFaces[g]]]

P Teeuwen · Answer 5 · 2024-03-06T10:46:46.753

You can use PlanarFaceList https://reference.wolfram.com/language/ref/PlanarFaceList.html

M = {{0, 1, 0, 0, 1, 1, 0, 0}, 
     {1, 0, 1, 0, 0, 0, 0, 1},  
     {0, 1, 0, 1, 0, 0, 1, 0}, 
     {0, 0, 1, 0, 1, 0, 1, 0}, 
     {1, 0, 0, 1, 0, 1, 0, 0}, 
     {1, 0, 0, 0, 1, 0, 0, 1}, 
     {0, 0, 1, 1, 0, 0, 0, 1}, 
     {0, 1, 0, 0, 0, 1, 1, 0}}
A = AdjacencyGraph[M, DirectedEdges -> False, GraphLayout -> "PlanarEmbedding", 
             VertexLabels -> "Name", ImagePadding -> 5];
Faces = PlanarFaceList[A]

Output = {{1, 2, 3, 4, 5}, {1, 5, 6}, {1, 6, 8, 2}, {2, 8, 7, 3}, {3, 7, 4}, {4, 7, 8, 6, 5}}

However, this includes the outer face.

Finding face vertices from the face adjacency graph

5 Answers5

Linked