The specific example can be solved with the help of finite Fourier cosine transform and its inversion:
With[{u = u[t, x]},
eq = D[u, t] == κ D[u, x, x];
ic = u == U[x] /. t -> 0;
bc = {D[u, x] == 0 /. x -> 0, D[u, x] == T /. x -> L};]
Format@finiteFourierSinTransform[f_, __] := Subscript[ℱ, s][f]
Format@finiteFourierCosTransform[f_, __] := Subscript[ℱ, c][f]
help[index_] :=
Module[{tset =
finiteFourierCosTransform[{eq, ic}, {x, 0, L}, index] /. Rule @@@ bc /.
HoldPattern@finiteFourierCosTransform[f_ /; ! FreeQ[f, u], __] :> f},
tsol = DSolve[tset, u[t, x], t][[1, 1, -1]]]
tsolgeneral = help[n]
tsolzero = help[0]
tsolfunc[n_] = Piecewise[{{tsolgeneral, n != 0}}, tsolzero]
sol = inverseFiniteFourierCosTransform[tsolfunc[n], n, {x, 0, L}] // transformToIntegrate

Let's check the solution numerically with $U=x(1-x),\ L=1,\ κ = 1,\ T = 1$:
U = (# (1 - #) &); L = 1; κ = 1; T = 1;
nsol = NDSolveValue[{eq, ic, bc}, u, {t, 0, 1/10}, {x, 0, 1},
Method -> {"MethodOfLines",
"DifferentiateBoundaryConditions" -> {True, "ScaleFactor" -> 5000}}];
With[{expr =
Block[{C = 20, HoldForm = Identity,
Sum = Function[{expr, lst}, Total@Table[expr, lst], HoldAll]}, sol]},
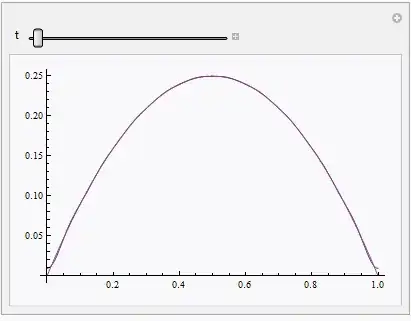
Manipulate[Plot[{expr, nsol[t, x]}, {x, 0, 1}, PlotRange -> All], {t, 0, 1/10}]]
Clear[U, L, κ, T]
Remark
Finite Fourier Cosine transform at $n=0$ is calculated separately here because currently finiteFourierCosTransform cannot handle the singularity at $n=0$ properly.
The reason why "DifferentiateBoundaryConditions" option is added is explained in this post.

