How to solve a 2D+1 PDE with a large convection term in stable and efficient way

Question

Follow from the discussion 2D+1 PDE problem

$\partial_t u(t,x,y)=-y\partial_{x}u+\partial_{y}\left[γ(1+sin(3x)) yu+A sin(3x)u+γkT(1+sin(3x))\partial_{y}u\right]$

with $u(0,x,y)=\frac{1}{2\pi}e^{-(x^2+y^2)/2}$

and periodic boundary condition:

$u(t,-\pi,y)=u(t,\pi,y)$

In $y$-direction, it is unbounded.

The code and result are shown below

a = 1;
T = 50;
ωb = -5; ωt = 5;
A = 1;
γ = .1;
kT = 0.1;
φ = 0;
mol[n_Integer, o_: "Pseudospectral"] := {"MethodOfLines", 
  "SpatialDiscretization" -> {"TensorProductGrid", "MaxPoints" -> n, 
    "MinPoints" -> n, "DifferenceOrder" -> o}}

With[{u = u[t,θ, ω]}, 
 eq = D[u, t] == -D[ω u,θ] - 
     D[-A Sin[3θ] u, ω] + γ (1 + 
        Sin[3θ])  kT  D[
       u, {ω, 2}] + γ  (1 + 
        Sin[3θ]) D[ω u, ω];
ic = u == E^(-((ω^2 +θ^2)/(2 a^2))) 1/(2 π a) /. 
    t -> 0];
ufun = NDSolveValue[{eq, ic, 
     u[t, -π, ω] == u[t, π, ω], 
     u[t,θ, ωb] == 0, u[t,θ, ωt] == 0}, 
    u, {t, 0, 
     T}, {θ, -π, π}, {ω, ωb, ωt}, 
    Method -> mol[35], MaxSteps -> Infinity]; // AbsoluteTiming
plots = Table[
    Plot3D[Abs[
      ufun[t,θ, ω]], {θ, -π, π}, {
ω, ωb, ωt}, AxesLabel -> Automatic, 
     PlotPoints -> 30, BoxRatios -> {Pi, ωb, 1}, 
     ColorFunction -> "LakeColors", PlotRange -> All], {t, 0, T, 
     1}]; // AbsoluteTiming
ListAnimate[plots]

The problem is if we increase the coefficient $A$ then the program is no longer stable. Simply refine the grid points are still not able to solve the problem entirely. Perhaps there is a smarter way to sample the grid points and time step, or?

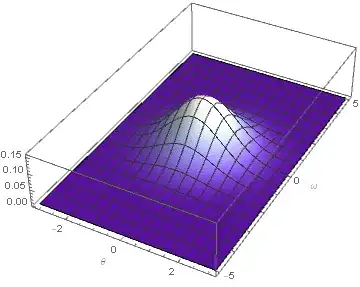
Result for $A=2$:

It's crazy..

Btw, since the x-direction is periodic but y is not, is it possible to use pseudospectral in x and keep the default setting for y?

Update (8/22)

Increasing A to 3 with MaxPoints=71 and MinPoints=51 still fails to converge. But my friend he can solve A=8 by Julia code with much fewer points less than a minute. There must be something wrong for my grids...

Note: The function u should be localized in 3 minima of potential $-\cos{3\theta}$.

Answer 1

It is necessary to increase the option "MaxPoints", for example, twice:

a = 1;
T = 50;
ωb = -5; ωt = 5;
A = 2;
γ = .1;
kT = 0.1;
φ = 0;
mol[n_Integer, o_: "Pseudospectral"] := {"MethodOfLines", 
  "SpatialDiscretization" -> {"TensorProductGrid", "MaxPoints" -> 2*n,
     "MinPoints" -> n, "DifferenceOrder" -> o}}

With[{u = u[t, θ, ω]}, 
  eq = D[u, t] == -D[ω u, θ] - D[-A Sin[3 θ] u, ω] + γ (1 + Sin[3 θ]) kT D[u, {ω, 2}] + γ (1 + Sin[3 θ]) D[ω u, ω];
  ic = u == E^(-((ω^2 + θ^2)/(2 a^2))) 1/(2 π a) /. 
    t -> 0];
ufun = NDSolveValue[{eq, ic, 
     u[t, -π, ω] == u[t, π, ω], 
     u[t, θ, ωb] == 0, u[t, θ, ωt] == 0}, 
    u, {t, 0, 
     T}, {θ, -π, π}, {ω, ωb, ωt}, 
    Method -> mol[35], MaxSteps -> Infinity]; // AbsoluteTiming
plots = Table[
    Plot3D[Abs[
      ufun[t, θ, ω]], {θ, -π, π}, {ω, ωb, ωt}, AxesLabel -> Automatic, 
     PlotPoints -> 30, BoxRatios -> {Pi, ωb, 1}, 
     ColorFunction -> "LakeColors", PlotRange -> All], {t, 0, T, 
     1}]; // AbsoluteTiming
ListAnimate[plots]

I give two tips on how to shorten the integration time by a factor of 10 and get rid of the large parameter A. First, we must divide all the terms of the equation into A. Secondly, we need to make the substitution t->T*t. Then the integration is always carried out on the interval (0,1), and the large parameter TA just normalizes the time derivative. We now make the normalization to gamma, then the divergence is completely eliminated. In addition, we need to add a new parameter q<<1 to exclude the degeneracy of the equation at the line $\sin (3\theta 0=-1).

K = 35; a = 1;
T = 1;
ωb = -5; ωt = 5;
A = 8;
γ = .1;
T0 = 50*A*γ;
kT = 0.1;
φ = 0;
q = 10^-5;
mol[n_Integer, o_: "Pseudospectral"] := {"MethodOfLines", 
  "SpatialDiscretization" -> {
   "TensorProductGrid", 
   "MaxPoints" -> 2*n, 
   "MinPoints" -> n, 
   "DifferenceOrder" -> o
   }
  };

With[{u = u[t, θ, ω]}, 
  eq = D[u, t]/T0 == -D[ω u, θ]/A/γ - D[-Sin[3 θ] u, ω]/γ + (1 + q*Sin[3 θ]) kT D[u, {ω, 2}] + (1 + q*Sin[3 θ]) D[ω u, ω];
  ic = u == E^(-((ω^2 + θ^2)/(2 a^2))) 1/(2 π a) /.  t -> 0
  ];
ufun = NDSolveValue[{eq, ic, 
     u[t, -π, ω] == u[t, π, ω], 
     u[t, θ, ωb] == 0, u[t, θ, ωt] == 0}, 
    u, {t, 0, 
     T}, {θ, -π, π}, {ω, ωb, ωt}, 
    Method -> mol[K], MaxSteps -> Infinity]; // AbsoluteTiming
plots = Table[
    Plot3D[Abs[
      ufun[t, θ, ω]], {θ, -π, π}, {ω, ωb, ωt}, 
      AxesLabel -> Automatic, 
      PlotPoints -> 30, ColorFunction -> "LakeColors", 
      PlotRange -> All
      ], 
     {t, 0, T, .1*T}]; // AbsoluteTiming
ListAnimate[plots]