11

The function

 s12 = 1/(Log[2^x]*((7.537/(x^2)) + (30.148/((2 + x)^3))))

returns expected function values for 0 < x < 10,000

but the graph drops to 0 at x = 1024.

I am using the home version 9.0. Am assuming operator error unless told otherwise, but an older version plots without problems.

Any advice welcome.

kglr
  • 394,356
  • 18
  • 477
  • 896
daniel
  • 519
  • 4
  • 12
  • 1
    Try Plot[s12,{x,0,2000},WorkingPrecision->20]. Also, please look through the editing help to learn how to format your code correctly. – sebhofer Jan 20 '13 at 21:58
  • Interestingly, redefining s12 to be a function dependent on some argument x and in turn plotting the new function results in a graph that does not drop to 0 without specifying the working precision. – VF1 Jan 20 '13 at 22:00
  • Both interesting comments. Will take the advice re formatting. My questions are usually basic so my ad hoc code has not been an issue to date. I see those days are over...Precision->20 worked, thanks. – daniel Jan 20 '13 at 22:02
  • 2
    @daniel Just an aside, in this case also WorkingPrecision->15 works, which is normally smaller than $MachinePrecision. That's because arbitrary precision arithmetic is taking over which is apparently able to handle this at low precision. In general one has to experiment a bit and see what value works... – sebhofer Jan 20 '13 at 22:06
  • @VF1 This is very funny indeed! – sebhofer Jan 20 '13 at 22:09
  • 2
    BTW using x*Log[2] - which is equivalent to your Log[2^x] - fixes the problem too. – Vitaliy Kaurov Jan 20 '13 at 22:13
  • It works without change to the expression if I set f[x_]=s12 and do Plot[f[x],{x,0,1030}]. – Jens Jan 20 '13 at 22:48
  • 2
    The fact that f[x_] works but s12 doesn't leads me to suspect that it's important for Plot to not evaluate the expression too early. E.g., if I replace f[x] by Evaluate[f[x]] in Plot, the error re-appears. But what is happening with the unevaluated expression? One thing it could be doing is some pre-processing for PlotLegends. And coincidentally, that's exactly what has changed in version 9. So I'm inclined to blame PlotLegends. Again!? Or should I blame units support... I like that idea too... – Jens Jan 20 '13 at 23:00
  • 1
    It works by setting the option Evaluated->False – Rojo Jan 20 '13 at 23:22
  • What I saw is just what @VF1 already wrote... and in addition it also works with Plot[s12/.x->y,{y,0,1030}] – Jens Jan 20 '13 at 23:38
  • 1
    @Jens excellent observation that it has to do with the sequence of evaluation - but how is that tied to the precision? This is why we need to know about internals. – VF1 Jan 21 '13 at 00:02

2 Answers2

9

This is only a possible explanation, so read with care. First, we should try to reduce the problem. What I was curious about was that it's exactly 1024 when the graph drops. Therefore I assumed it must be connected to the Log and the 2^x inside, and indeed look at this

Plot[1/Log[2^2^x], {x, 9.5, 10.5}]

(I used 2^x so that the critical point is at 10.0)

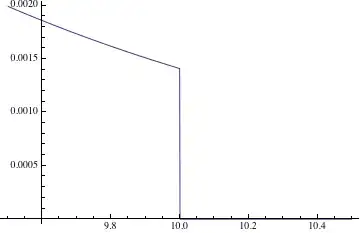
Mathematica graphics

What I assume is that Mathematica compiles the expressions if possible. One could look at the Trace of such a Plot to see how many checks are done to find out, what kind of function is supplied and whether it has discontinuities etc. Beside other things, one can find options for Compile in the trace too. Let's try it

f = Compile[{{x, _Real}}, 1/Log[2^2^x]]
Table[f[x], {x, 10 - 10^-6, 10 + 10^-6, 10^-7}]
(*
  {0.00140888, 0.00140888, 0.00140888, 0.00140888,
   0.00140888, 0.00140888, 0.00140888, 0.00140888, 0.00140888, 
   0.00140888, 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.}
*)

This confirms the assumption and of course the plot of f[x] has the same drop.

The conclusion could be that Mathematica compiles expressions if possible. Obviously, defining a function with g[x_]:=.. or using the Evaluated option does prevent this from happening.

As an additional note, @sebhofer mentioned in the first comment

Try Plot[s12,{x,0,2000},WorkingPrecision->20].

The question is, why does this work? Real numbers as used in compiled expressions have $MachinePrecision which is a value around 16. Try to set WorkingPrecision to 5 and you see that it's working anyway. The reason is in my opinion, that setting WorkingPrecision to any other value than MachinePrecision does prevent the call to Compile. Try it yourself

Plot[1/Log[2^2^x], {x, 9.5, 10.5}, WorkingPrecision -> #] & /@ {5, 20, MachinePrecision}
halirutan
  • 112,764
  • 7
  • 263
  • 474
  • Just a small comment: 64-bit IEEE floating point presentation ("machine reals") has maximum value presentable, non-infinite value just under 2^1024. This is the reason why compiled/machine precision arithmetic fails at this point. – kirma Jul 19 '13 at 05:13
4

Another solution, which tends to confirm @halirutan's explanation, is that the following produces the correct graph when compilation is turned off.

Plot[1/(Log[2^x]*((7.537/(x^2)) + (30.148/((2 + x)^3)))), {x, 0, 1200}, Compiled -> False]

Another confirmation is that if we turn on the tracking of machine overflow, we get the following:

cf = Compile[x, 1/(Log[2^x]*((7.537/(x^2)) + (30.148/((2 + x)^3)))), 
  RuntimeOptions -> {"CatchMachineOverflow" -> True}]

During evaluation of In[25]:= CompiledFunction::cfn: Numerical error encountered at instruction 1; proceeding with uncompiled evaluation. >>

(* Out[25]= 195.251 *)

The expression cf[x] will produce the correct plot as well.

Update

From Compiling Mathematica Expressions:

Similarly, functions like Plot and Plot3D use Compile on the expressions you ask them to plot. Built-in functions that use Compile typically have the option Compiled. Setting Compiled -> False tells the functions not to use Compile.

Michael E2
  • 235,386
  • 17
  • 334
  • 747