4

I don't know if this issue has been discussed before, if anyone know any related post, please let me know, thank you :)

Unprotect the function Sin and create a new definition for it:

Unprotect[Sin];
Sin[x_] := x^2;

Because x_ matches any expression, then I think (naively) the system definition of Sin would never be applied. 

{Sin[2], Sin[1.2], Sin[Sin]}
(*
   {4, 1.44, Sin^2}
*)

Every thing works as expected except for Plot:

Plot[Sin[x], {x, 0, Pi}]

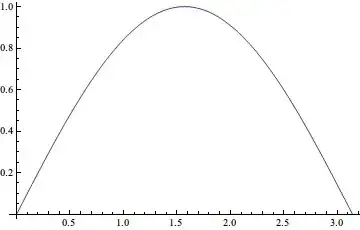
enter image description here

I think it's related to the internal computation of Plot, I checked the mass output of Trace and found nothing useful.

I know it's stupid to modify a system symbol this way, but could you please give me some explanation? Thanks in advance.

mmjang
  • 2,583
  • 20
  • 26
  • 6
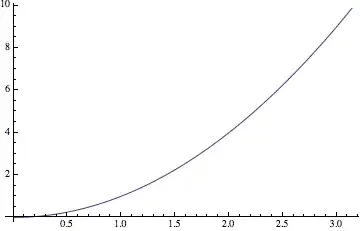
    Part of the reason why modifying system symbols is such a bad idea is that they aren't bound to follow the same rules as ordinary symbols. In this case your modification was successful in one case and not another, suggesting that the behavior of Sin is to some extent hard-coded in the system. Modifying system symbols in such a way as to contradict their usual behavior carries the risk that your modifications may be unpredictably reverted at any time. – Oleksandr R. Jul 15 '13 at 03:13
  • 4
    In this specific case, Plot[Evaluated@Sin... works, but Oleksandr's point is valid nevertheless. – rm -rf Jul 15 '13 at 03:51
  • 2
    I thought it might have to do with compilation (Compile your Sin and you get sine). But Method -> {Compiled -> False} yields a sine curve. However, Plot[Sin[x], {x, 0, 10}, WorkingPrecision -> 10] and Plot[(If[,,]; Sin[x]), {x, 0, 10}] yield parabolas; but Plot[(If[True,,]; Sin[x]), {x, 0, 10}] yields sine. Curious. But I, too, think Oleksandr is on target. – Michael E2 Jul 15 '13 at 06:07

1 Answers1

8

I figured out that the Compiled reference page has the usage wrong,* which misled my interpretation of the results of Plot. Indeed I think the explanation is that Plot compiles the function expression. In the compiled version, it makes internal calls to sine, which is the real sine, not your Sin. It circumvents the normal pattern matching because it assumes System` functions are in fact system functions. (I might rephrase OleksandrR's comment this way: system functions are in the context "System`" for a reason.)

In any case, this "fixes" your plot:

Plot[Sin[x], {x, 0, Pi}, Compiled -> False]

Mathematica graphics

*The example should read

Plot[If[Exp[-x] == 0., 0, -1] + x/900, {x, 0, 1000}, Compiled -> False]

The syntax highlighting will mark Compiled in red, but it works nonetheless, as implied in Compiling Mathematica Expressions:

Similarly, functions like Plot and Plot3D use Compile on the expressions you ask them to plot. Built-in functions that use Compile typically have the option Compiled. Setting Compiled -> False tells the functions not to use Compile.

Michael E2
  • 235,386
  • 17
  • 334
  • 747