If I use FullSimplify on a large formula it will consequently return a much smaller expression. However, suppose I notice the simplified expression can benefit from further intermediate definitions. For example, say I observe c = (1-a)(1-b), would make my expression drastically smaller.
Instead of spending time to try such substitutions, does Mathematica have functionality to perform this work for me? More particularly, how would I find optimal sub-expressions to simplify the following expression?
(1/(a^2 (b + m)))(-(-1 + a + 2 b) (-1 + 2 b + 2 m) - 4 b ArcTanh[1 - 2 b] + Log[4] + 2 ((2 + a) b + m + a m) Log[1 + a] - a (b + m) Log[4 - 4 b] + a Log[(2 - 2 b)/(1 + a)] - m Log[1 - b] + 2 Log[(1 - b)/(1 + a)] + (m - a (b + m)) Log[b])

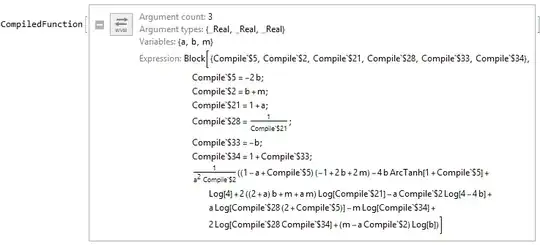
Experimental`OptimizeExpressioncan look for common subexpressions, but it won't change the way the expression is written to expose more such subexpressions. I believe it is meant for speeding up computations (avoid computing the same thing twice), not for simplification. BTW +1, I wished for such a feature many times. – Szabolcs Sep 13 '18 at 14:48Compile[]is also able to find common subexpressions if the whole expression is compilable in general. The resultingCompiledFunctioncontains a list of imperative program steps that is equal to the original expression. – Thies Heidecke Sep 17 '18 at 16:46