Thick polygons in Graphics3D

Question

I have a polygon that I want to thicken with thickness h. How do I do this?

FaceForm is evil and says:

The directive Thickness was encountered in a context where it is not allowed.

Closely related: How to extrude a 3D image from a binary 2D image — Mr.Wizard, Jan 21 '13 at 23:17

jVincent · Accepted Answer · 2013-01-22T23:16:34.900

Similar to ssch's method, but I though I'd throw in mine, it' just finds the normal of the polygon (The average normal if the polygon isn't planar). It then moves the polygon along this direction to create a top and bottom polygon, and then fill in the sides between these two:

normal[a_,b_,c_]:=Normalize@Cross[a-b,c-b]
normal[a___]:=Mean[normal@@@Partition[{a},3,1,1]]

sides[bottom_,top_] :=     
   Polygon[Reverse@Join[#1,Reverse@#2]]&@@@({bottom,top}//Transpose//Partition[#,2,1,1]&)

thicken[val_,t_:0.1]:=val/.Polygon[bottom_,___]:>
 With[{top=(# +t normal@@bottom)&/@bottom},
    {Polygon[Reverse@bottom],
     sides[bottom,top],
     Polygon[top]
    } 
 ]

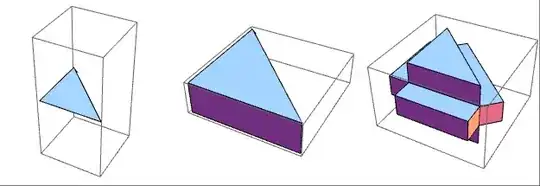
Applying multiple times can lead to fun results:

initial = 
Graphics3D[{Arrow@{{0, 0, 0}, {1, 0, 0}, {0, 1, 0}}, 
Polygon[{{0, 0, 0}, {1, 0, 0}, {0, 1, 0}}]}];
NestList[thicken[#, 0.3] &, initial, 2] // GraphicsRow

Illustration of the function applied multiple times to a simple triangle

To use this with graphics generated by for instance Plot3D, you simply have to use Normal to expand out GraphicsComplex's. I also added a slight pattern above (The second part of Polygon[bottom_,___]) which makes the code ignore anything in polygon after the points. This is nessesary because some graphics include normals which are not accounted for above:

(Normal@Plot3D[Cos[x] Cos[y], {x, 0, \[Pi]}, {y, 0, \[Pi]}, 
 Mesh -> None, PlotPoints -> 2]) // thicken[#, 0.3] &

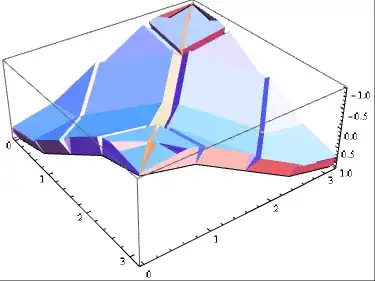
Thicken function applied to output from Plot3D

Should be more funny if applicable for Graphics3D generated by Plot3D etc. :) — Silvia, Jan 22 '13 at 16:53
@Silvia The only reason it didnt' before was because Plot3D returns a result using GraphicsComplex, and because the polygons have normals. I've updated with a small change in the pattern so it'll ignore normal and a small example of how to use output form Plot3D. — jVincent, Jan 22 '13 at 23:17
That is great! I did something like this with your function :) — Silvia, Jan 23 '13 at 00:25

ssch · Answer 2 · 2013-01-22T00:31:23.530

Layering:

By creating a bunch of the same polygon at slightly different heights on top of each other the effect can be simulated:

(* Same as Table but high is always included*)
Attributes[tableEnsureUpper]=HoldAll;
tableEnsureUpper[expr_, {sym_, low_, high_, step_: 1}] := 
 If[Mod[high - low, step, step] == step,
  Table[expr, {sym, low, high, step}],
  Append[Table[expr, {sym, low, high, step}],Block[{sym=high}, expr]]
  ]
(* Expects 2D Polygon in *)
raisePolygonLayered[p_Polygon, h_: 1] := 
 tableEnsureUpper[
  p /. {a_?NumericQ, b_?NumericQ} :> {a, b, z}, {z, 0, h, 0.2}]

layered

Problems is that the slices are visible from the side unless very many are used.

Edge Polygon

The method is based on taking each successive (overlapping) pair of points and creating the corresponding rectangle with height h:

raisePolygonEdge[p_Polygon, h_: 1] := Module[{
   data = p[[1]],
   pts
   },
  If[Depth[data] == 3, data = {data}];
  pts = Flatten[Partition[Riffle[Most@#, Rest@#], 2] & /@ data, 1];
  Polygon[ Join[{ 
       {#[[1, 1]], #[[1, 2]], 0}, {#[[1, 1]], #[[1, 2]], h},
       {#[[2, 1]], #[[2, 2]], h}, {#[[2, 1]], #[[2, 2]], 0}
       } & /@ pts, data /. {a_?NumericQ, b_?NumericQ} :> {a, b, h}]]
  ]

edged

The edge method is what I used in this answer, although it was simpler there since the polygon was regular. — rm -rf, Jan 21 '13 at 23:18

score 1 · Answer 3 · edited Apr 13 '17 at 12:56

I've already answered something like this here, but here's a slightly simplified version you might find useful:

(* barycenter of a polygon *)
averagepoints[points_?MatrixQ] :=
        Mean[If[TrueQ[First[points] == Last[points]], Most, Identity][points]]

(* Newell's algorithm for face normals *)
newellNormals[pts_?MatrixQ] := Module[{tp = Transpose[pts]}, Normalize[MapThread[Dot,
              {RotateLeft[ListConvolve[{{-1, 1}}, tp, {-1, -1}]], 
               RotateRight[ListConvolve[{{1, 1}}, tp, {-1, -1}]]}]]]

thickenaux[points_, thick_] := Module[{center = averagepoints[points],
  nrm = newellNormals[points], outerpoints, radialpoints}, 
  outerpoints = Map[TranslationTransform[thick nrm], points];
  radialpoints = MapThread[Join[#1, Reverse[#2]] &,
                           Map[Partition[#, 2, 1, 1] &, {points, outerpoints}]];
  Flatten[{Polygon[Reverse[points]], Polygon /@ radialpoints, Polygon[outerpoints]}]]

ThickenPolygons[shape_, thick_: 0.04] :=
       shape /. Polygon[p_?MatrixQ] :> thickenaux[p, thick]

Examples:

NestList[ThickenPolygons,
         Graphics3D[Polygon[{{0, 0, 0}, {1, 0, 0}, {0, 1, 0}}]], 2] // GraphicsRow

jVincent's example

PolyhedronData["Tetrahedron"] // Normal // ThickenPolygons

"thickened" tetrahedron

Thick polygons in Graphics3D

3 Answers3

Linked