3

I encounter this very often, here is just one recent example: I want

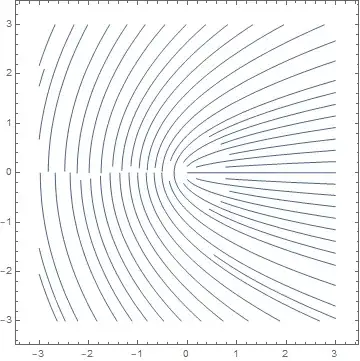
StreamPlot[ReIm[Sqrt[x+I y]],{x,-3,3},{y,-3,3},StreamStyle->"Line"]

and because of square root ambiguity get this unpleasant slit on the left:

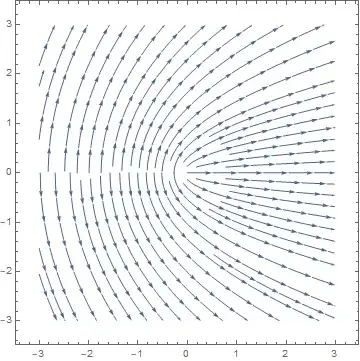
enter image description here

Doing this with arrows reveals the reason -

enter image description here

Having seen this I managed to figure out how to fill the gap,

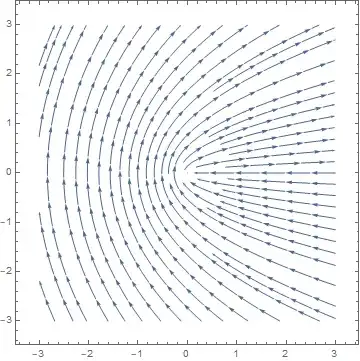
StreamPlot[{Sign[y]Sqrt[(Sqrt[x^2+y^2]+x)/2],Sqrt[(Sqrt[x^2+y^2]-x)/2]},{x,-3,3},{y,-3,3}]

gives what I want, namely

enter image description here

However this is clearly ad hoc and clumsy, and also there are more complicated cases where I don't know how to proceed, like e. g. those ugly white crosses in

ContourPlot[Arg[JacobiCN[x+I y,1/2]],{x,-5,5},{y,-5,5},ColorFunction->Hue]

enter image description here

Is there some uniform remedy for such cases?

მამუკა ჯიბლაძე
  • 2,066
  • 14
  • 27
  • 2
    It doesn't really fix your problem, but it looks better ContourPlot[Arg[JacobiCN[x + I y, 1/2]], {x, -5, 5}, {y, -5, 5}, ColorFunction -> Hue, ExclusionsStyle -> Red] – mikado Sep 30 '18 at 13:33
  • 1
    I think Riemann was the first to study this problem seriously. See, for instance, (1000973). It's not real clear to me how general an answer you want. On the one hand, you seek to remove the discontinuities of discontinuous functions, which seems impossible in general. It is possible in the two examples because of a certain coincidence or symmetry between the discontinuity and the image desired. – Michael E2 Sep 30 '18 at 14:06
  • @MichaelE2 I agree that the question is not well enough formulated. Indeed I had in mind so to say "removable" discontinuities - i. e. when what I want to plot is actually continuous. It is slightly tricky in the first example: discontinuity is actually not removable there, but one can drag the line of discontinuity around, and what I did was to move it from the negative to the positive horizontal half-axis: in this way it is not visible in the plot since the flow lines are parallel to it near it. – მამუკა ჯიბლაძე Sep 30 '18 at 14:22
  • I don't ever remember that there was a general method to patch through discontinuities. There was always an element of art involved... – J. M.'s missing motivation Sep 30 '18 at 14:54
  • 1
    related: How to plot real roots of complex polynomials avoiding branch cuts?. – AccidentalFourierTransform Sep 30 '18 at 15:28
  • @J.M.issomewhatokay. At least for the square root, the following must be possible: if ambiguity is only in the direction (like with the square root), I would like to plot curves tangent to a given field of (directionless) line elements (i. e. a differential form). As for Arg, I believe ColorFunction -> Hue should be able to remove any ambiguity involved, no? – მამუკა ჯიბლაძე Sep 30 '18 at 18:58
  • 1
    If you're just using Hue[] to visualize phase, then yes, Hue[] along with Exclusions -> None ought to do it. – J. M.'s missing motivation Oct 01 '18 at 20:04

0 Answers0