I had a more general question about a similar problem more than two years ago, Getting rid of discontinuities in plots caused by square roots, logarithms, `Arg`, etc, which got lots of interesting feedback but no definite answer.
So I decided to focus on something more obviously urgent and simple.
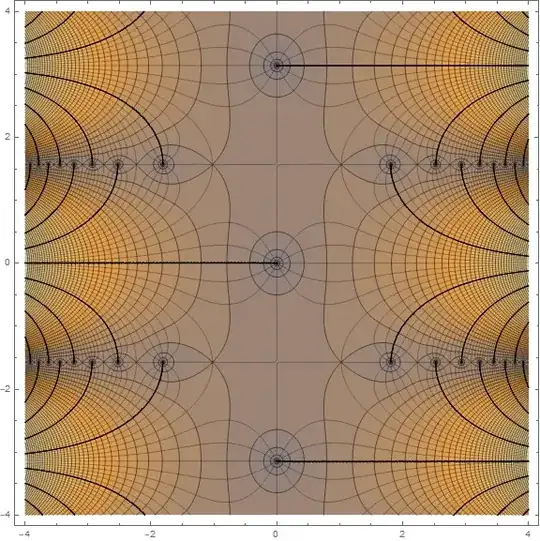
Here is the result of
ContourPlot[Log[Abs[Sinh[Sinh[x+I y]]]],{x,-4,4},{y,-4,4},
MeshFunctions->{Arg[Sinh[Sinh[#1+I #2]]]&},
Mesh->11,PlotPoints->150,Contours->50]
I guess I don't even need to ask: I want to get rid of those rough thick black lines, that's all.
PS Heard rumours that it might be incorporated in version 12. I have 11.0.1.0, but still, let me know if this is the case.
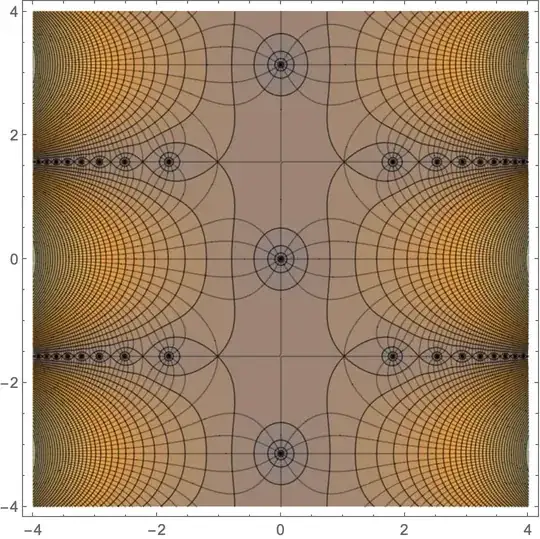
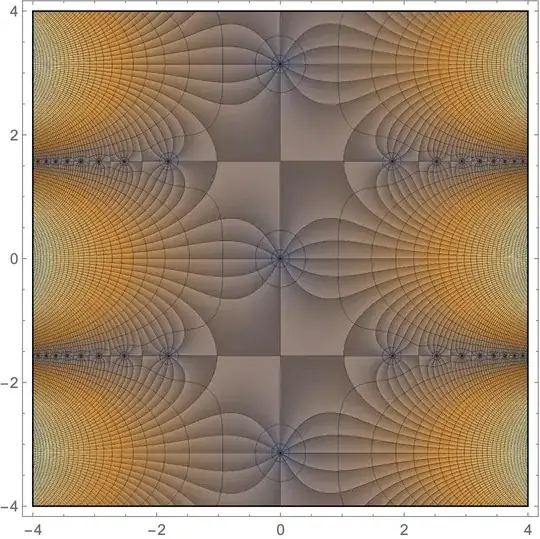
MeshFunctionsshould be continuous. Discontinuities lead to such ugly streaks. – Michael E2 Feb 02 '21 at 19:06