Adding overlapping non-weighted, directed edges to a weighted, undirected graph

Question

I have the following Mathematica code based on the GDB1 instance from the CARP literature:

HighlightGraph[
 Graph[{1 \[UndirectedEdge] 2, 1 \[UndirectedEdge] 4, 
   1 \[UndirectedEdge] 7, 1 \[UndirectedEdge] 10, 
   1 \[UndirectedEdge] 12 , 2 \[UndirectedEdge] 3, 
   2 \[UndirectedEdge] 4, 2 \[UndirectedEdge] 9, 
   3 \[UndirectedEdge] 4, 3 \[UndirectedEdge] 5, 
   5 \[UndirectedEdge] 6, 5 \[UndirectedEdge] 11, 
   5 \[UndirectedEdge] 12, 6 \[UndirectedEdge] 7, 
   6 \[UndirectedEdge] 12, 7 \[UndirectedEdge] 8, 
   7 \[UndirectedEdge] 12, 8 \[UndirectedEdge] 10, 
   8 \[UndirectedEdge] 11, 9 \[UndirectedEdge] 10, 
   9 \[UndirectedEdge] 11, 10 \[UndirectedEdge] 11}, 
  EdgeWeight -> {13, 17, 19, 19, 4, 18, 9, 2, 20, 5, 7, 20, 11, 4, 3, 
    8, 18, 3, 10, 16, 14, 12}, EdgeStyle -> Thick, 
  VertexLabels -> Table[i -> Placed[i, Center], {i, 12}], 
  VertexLabelStyle -> Directive[White, Bold, 15], VertexSize -> 0.6, 
  GraphLayout -> {"VertexLayout" -> {"SpringElectricalEmbedding", 
      "EdgeWeighted" -> True}}], {1, Red}]

Which outputs the following weighted graph:

On which I would like to display multiple manually entered directed routes starting and ending at the highlighted vertex 1. These routes can overlap, traversing each edge multiple times, requiring multiple distinct directed arcs between nodes. However, they cannot also be introduced as weighted edges or they will distort the topology of the graph.

I will discern different routes with different coloured edges, so being able to make a single class of different edges between nodes will suffice.

I'm stumped. Any thoughts on how to do this would be fantastic.

EDIT: see post on colouring/formatting of edges here: Weighted graph with multiple different coloured non-weighted paths - styling

Answer 1

g1 = Graph[{1 <-> 2, 1 <-> 4, 1 <-> 7, 1 <-> 10, 1 <-> 12 , 2 <-> 3, 
       2 <-> 4, 2 <-> 9, 3 <-> 4, 3 <-> 5, 5 <-> 6, 5 <-> 11,  5 <-> 12, 6 <-> 7, 
       6 <-> 12, 7 <-> 8,  7 <-> 12, 8 <-> 10, 8 <-> 11, 9 <-> 10,  9 <-> 11, 10 <-> 11}, 
     EdgeWeight -> {13, 17, 19, 19, 4, 18, 9, 2, 20, 5, 7, 20, 11, 4,  3, 
         8, 18, 3, 10, 16, 14, 12}, EdgeStyle -> Thick, 
     VertexLabels -> Table[i -> Placed[i, Center], {i, 12}], 
     VertexLabelStyle -> Directive[White, Bold, 15], 
     VertexSize -> 1, 
     GraphLayout -> {"VertexLayout" -> {"SpringElectricalEmbedding", 
             "EdgeWeighted" -> True}}] ;

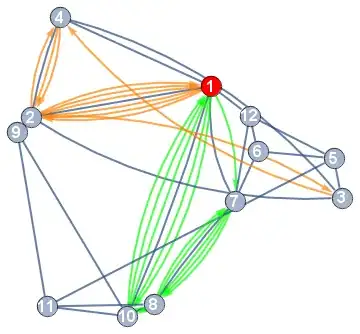
path = {1, 2, 3, 4, 2, 4, 2, 1, 2, 1, 2, 1};
newedges = DirectedEdge @@@ Partition[path, 2, 1];
g2 = SetProperty[EdgeAdd[g1, newedges], {VertexCoordinates -> GraphEmbedding[g1], 
   VertexStyle -> {1 -> Red}, 
   EdgeStyle -> {Alternatives @@ newedges -> Orange}}] 

Update: for multiple paths

path1 = {1, 2, 3, 4, 2, 4, 2, 1, 2, 1, 2, 1};
path2 = {1, 7, 8, 7, 8, 7, 8, 10, 8, 10, 1, 10, 1, 10, 1};
newedges1 = DirectedEdge @@@ Partition[path1, 2, 1];
newedges2 = DirectedEdge @@@ Partition[path2, 2, 1]; 
g3 = SetProperty[EdgeAdd[g1, Join[newedges1, newedges2]], 
 {VertexCoordinates -> GraphEmbedding[g1], VertexStyle -> {1 -> Red}, 
 EdgeStyle -> {Alternatives @@ newedges1 -> Orange, Alternatives @@ newedges2 -> Green}}]