Graph: Coloring parallel edges individually

Question

CODE:

Graph[{Style[0 -> 1, Red], Style[0 -> 1, {Blue, Dashed}]}]

This Mathematica code will make both lines solid Red, since they belong to the same two vertices and have the same direction.

I want one of them to be red, the other blue dashed for instance. How can I do this?

Answer 1

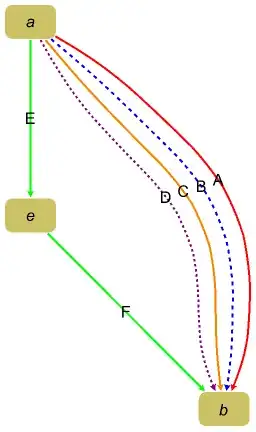
Update 3: With the new-in-version-12.1 function EdgeTaggedGraph we can style and label edges individually in multi-graphs:

labels = {"A", "B", "C", "D", "E", "F"};
edges = {a -> b, a -> b, a -> b, a -> b, a -> e, e -> b};
styles = {Red, Directive[Dashed, Blue], Orange, 
   Directive[Purple, Dashing[.01]],  Green, Green};

labelededges = MapThread[Style[Labeled[#, #2], #3] &, {edges, labels, styles}] ;

EdgeTaggedGraph[labelededges, EdgeLabels -> "Name", 
 ImageSize -> Medium, BaseStyle -> Thick, EdgeLabelStyle -> 16, 
 VertexLabelStyle -> 16, PlotTheme -> "DiagramGold"]

Update 2: A much more convenient approach to construct a custom EdgeShapeFunction to style multi-edges individually:

styles = Association[PropertyValue[g1, EdgeStyle]] ;
esf = {Dashing[{}], First[styles[#2] = RotateRight[styles[#2]]], 
   Arrowheads[Large], Arrow[#, .1]} &;
Graph[g1, EdgeShapeFunction -> esf]

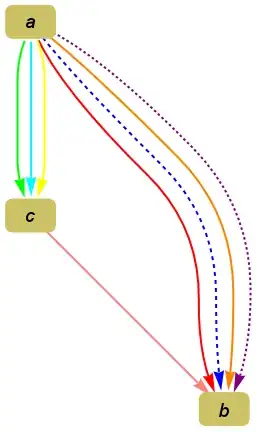
Update: To make it more convenient to specify precisely the color (style) of each edge in a multigraph, not resort to a fixed sequence of styles as suggested by @David G Stork in the comments:

Specify edge labels for each edge using EdgeStyle:

g1 = Graph[{a -> b, a -> b, a -> b, a -> b, a -> c, a -> c, a -> c, c  -> b}, 
VertexLabelStyle -> 18, VertexLabels -> Placed["Name", Center],
GraphLayout -> "LayeredDigraphEmbedding", GraphStyle -> "DiagramGold",
EdgeStyle -> {(a -> b) -> {Red, Directive[Dashed, Blue], Orange, 
 Directive[Purple, Dashing[.01]]},
 (a -> c) -> {Green, Cyan, Yellow}, (c -> b) -> {Pink}}];

In g1 multi-edges are colored with a single color.

Extract the styles for desired edge (e) into the variable style[e], and initialize the variable index[e] to 1.

ClearAll[index, style]
distinctedges = DeleteDuplicates[EdgeList[g1]];
(style[#] = PropertyValue[{g1, #}, EdgeStyle])& /@ distinctedges;
(index[#] = 1) & /@  distinctedges;

Inject the multiple styles for each edge using EdgeShapeFunction:

g2 = Fold[(SetProperty[{#,  #2}, EdgeShapeFunction -> 
  ({Arrowheads[Large], Thick, style[#2][[index[#2]++]], Arrow[#, .1]} &)]) &, 
   g1,  distinctedges];

Row[{g1, g2}]

Original answer:

You can use EdgeShapeFunction:

styles={Red, Directive[Dashed, Blue], Orange, Directive[Purple, Dashing[.01]], 
        Green, Green};
i = 1; 
Graph[{a -> b, a -> b, a -> b, a -> b, a -> e, e -> b},  
EdgeShapeFunction -> ({Arrowheads[Large],Thick,styles[[i++]],Arrow@#} &),
VertexLabels->"Name"] 

If you have at most two edges between a pair of vertices, you can also cheat using the Arrowheads option:

Graph[{Style[0 -> 1, {Arrowheads[.04], Red}], Style[1 -> 0,
   {Blue, Arrowheads[{-.04, 0.}], Dashed}], 0 -> 2, 2 -> 1},
 VertexLabels -> "Name", ImagePadding -> 10]