ElementMesh from ImplicitRegion cuts corners of region

Question

I'm trying to define a region within a cell and below a level set of a function using ImplicitRegion and ToElementMesh.

Here I define the cell

basis = {{1.3, 3.4}, {3.8, 1.1}}/2;
offset = {0, 0};
cell = Parallelogram[offset, Transpose[basis]];
Graphics[{Transparent, EdgeForm[Thick], cell}]

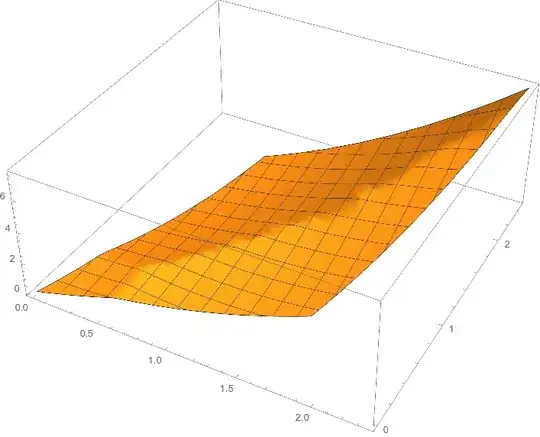
Here is the function definition.

f[x_, y_, n_] := RankedMin[Eigenvalues[ { {(x)^2 + (y)^2, .1, 0, 0, 0},
                                          {.1, (x + 1)^2 + (y)^2, .1, 0, 0},
                                          {0, .1, (x - 1)^2 + (y)^2, .1, 0},
                                          {0, 0, .1, (x)^2 + (y + 1)^2, .1},
                                          {0, 0, 0, .1, (x)^2 + (y - 1)^2} } ], n];
Plot3D[f[x, y, 1], {x, y} \[Element] cell]

Here I create the region

<< NDSolve`FEM`
reg = ToElementMesh[ ImplicitRegion[ f[x, y, 1] < 10 && {x, y} \[Element] cell, {x, y}]];

To test that the region was accurate, I set the isovalue of the level set to 10. The expected area is then just the area of the cell, but it's off by a bit.

Total[reg["MeshElementMeasure"], 2] - Abs[Det[basis]]
-0.000564115

From a plot of the region you can see that the top-left and lower-right corners are getting cut off.

Show[RegionPlot[reg], Graphics[{Transparent, EdgeForm[Thin], cell}]]

Is there a way I can compute an ElementMesh that can accurately represent this region to within 15 decimals?

I have tried increasing AccuracyGoal, setting "BoundaryMeshGenerator" -> "Continuation", decreasing the size of MaxBoundaryCellMeasure and MaxCellMeasure, and setting MeshQualityGoal -> Maximal.

Did the answer I wrote help you? – user21 Oct 23 '18 at 12:13 — user21, Oct 23 '18 at 12:13
Yes, that fixed my problem. Thanks! – jerjorg Oct 23 '18 at 16:46 — jerjorg, Oct 23 '18 at 16:46

score 3 · Accepted Answer · answered Oct 20 '18 at 15:27

Here is a way to proceed. The idea is to mesh the regions separately and then find the intersection. However, I do not see a way to get 15 digits of precision.

basis = {{1.3, 3.4}, {3.8, 1.1}}/2;
offset = {0, 0};
cell = Parallelogram[offset, Transpose[basis]];
(*Graphics[{Transparent,EdgeForm[Thick],cell}]*)

f[x_, y_, n_] := 
  RankedMin[
   Eigenvalues[{{(x)^2 + (y)^2, 1/10, 0, 0, 
      0}, {1/10, (x + 1)^2 + (y)^2, 1/10, 0, 0}, {0, 
      1/10, (x - 1)^2 + (y)^2, 1/10, 0}, {0, 0, 
      1/10, (x)^2 + (y + 1)^2, 1/10}, {0, 0, 0, 
      1/10, (x)^2 + (y - 1)^2}}], n];
(*Plot3D[f[x,y,1],{x,y}\[Element]cell]*)


<< NDSolve`FEM`
rmf = RegionMember[cell];
r1 = ImplicitRegion[rmf[{x, y}], {x, y}];
r2 = ImplicitRegion[f[x, y, 1] < 10, {x, y}];
mr1 = MeshRegion[ToElementMesh[r1, "MeshOrder" -> 1]];
mr2 = MeshRegion[
   ToElementMesh[r2, RegionBounds[cell], "MeshOrder" -> 1]];
reg = ToElementMesh[RegionIntersection[mr1, mr2]];
Total[reg["MeshElementMeasure"], 2] - Abs[Det[basis]]

-7.62945*10^-13

Let me know if that is a viable solution.

The above method with different regions to fit my problem crashes the kernel with no error messages :( — user1816847, Oct 29 '19 at 19:07

ElementMesh from ImplicitRegion cuts corners of region

1 Answers1

Linked