Holes in ElementMesh with ToElementMesh of ImplicitRegion

Question

I am trying to plot a function in a region below a level curve of the function and within a cell. I have been doing this by calculating an ElementMesh using ImplicitRegion and ToElementMesh, but the result is inaccurate.

Here is the cell (it's just a square),

cell = Parallelogram[{-0.5`, -0.5`}, {{1.`, 0.`}, {0.`, 1.`}}];
Graphics[{Transparent, EdgeForm[Thick], cell}]

and the function,

f[kx_, ky_, n_] := 
  Sort[Eigenvalues[{{(-1. + kx)^2 + (-1. + ky)^2, -0.23, 0., -0.23, 
       0.12, 0., 0., 0., 
       0.}, {-0.23, (-1. + kx)^2 + (0. + ky)^2, -0.23, 0.12, -0.23, 
       0.12, 0., 0., 0.}, {0., -0.23, (-1. + kx)^2 + (1. + ky)^2, 0., 
       0.12, -0.23, 0., 0., 0.}, {-0.23, 0.12, 
       0., (0. + kx)^2 + (-1. + ky)^2, -0.23, 0., -0.23, 0.12, 
       0.}, {0.12, -0.23, 
       0.12, -0.23, (0. + kx)^2 + (0. + ky)^2, -0.23, 0.12, -0.23, 
       0.12}, {0., 0.12, -0.23, 0., -0.23, (0. + kx)^2 + (1. + ky)^2, 
       0., 0.12, -0.23}, {0., 0., 0., -0.23, 0.12, 
       0., (1. + kx)^2 + (-1. + ky)^2, -0.23, 0.}, {0., 0., 0., 
       0.12, -0.23, 
       0.12, -0.23, (1. + kx)^2 + (0. + ky)^2, -0.23}, {0., 0., 0., 
       0., 0.12, -0.23, 0., -0.23, (1. + kx)^2 + (1. + ky)^2}}]][[
   n]];
Plot3D[f[x, y, 4], {x, y} \[Element] cell, PlotPoints -> 50]

and what the region should look like,

isovalue = 1.29897233417072;
ContourPlot[f[x, y, 4], {x, y} \[Element] cell, 
 Contours -> {isovalue}, ColorFunction -> GrayLevel, 
 PlotPoints -> 100]

This is what I have tried

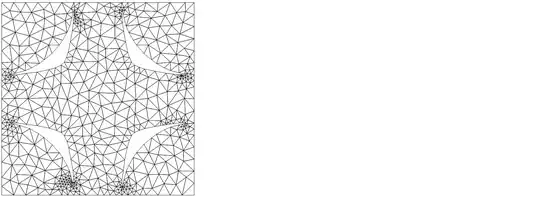
reg = ToElementMesh[
   ImplicitRegion[
    f[x, y, 4] < isovalue && {x, y} \[Element] cell, {x, y}], 
   "MaxBoundaryCellMeasure" -> 0.01, MeshQualityGoal -> 1, 
   PerformanceGoal -> "Quality", MaxCellMeasure -> 0.01, 
   "BoundaryMeshGenerator" -> "Continuation"];
RegionPlot[reg]

The region is no more accurate when I decrease MaxCellMeasure or MaxBoundaryCellMeasure. I also tried the solution suggested here.

score 5 · Answer 1 · answered Apr 25 '19 at 04:55

I hope I interpreted your question correctly that you want a more accurate ElementMesh representation of the region.

First we create a high quality Graphics of the region of interest.

isovalue = 1.29897233417072;
(* Add some margins to plot range to get connected region. *)
tolerance = 0.05;
plot = ContourPlot[
  f[x, y, 4],
  {x, y} ∈ Cuboid[{-0.5, -0.5} - tolerance, {0.5, 0.5} + tolerance],
  Contours -> {isovalue},
  ColorFunction -> GrayLevel,
  (* We need high quality plot for ImageMesh later. *)
  PlotPoints -> 200,
  Frame -> None
]

Create MeshRegion from Graphics object.

mreg = ImageMesh[ColorNegate[plot]]

And convert it to ElementMesh.

Needs["NDSolve`FEM`"]
mesh = ToElementMesh[mreg,"MeshOrder"->1]
(* ElementMesh[{{7., 353.}, {7., 353.}}, {TriangleElement["<" 1057 ">"]}] *)

mesh["Wireframe"]

score 5 · Accepted Answer · answered Apr 25 '19 at 05:33

Another approach is:

reg = ToElementMesh[
   ImplicitRegion[
    f[x, y, 4] < isovalue && {x, y} \[Element] cell, {x, y}], 
   "MaxBoundaryCellMeasure" -> 0.01, MeshQualityGoal -> 1, 
   PerformanceGoal -> "Quality", MaxCellMeasure -> 0.01, 
   "BoundaryMeshGenerator" -> {"RegionPlot", "SamplePoints" -> 41}];

reg["Wireframe"]

One thing to be a bit careful about is the question if the holes intersect the boundary. From the mesh it does not look like it but the math might say it.

Holes in ElementMesh with ToElementMesh of ImplicitRegion

2 Answers2