2

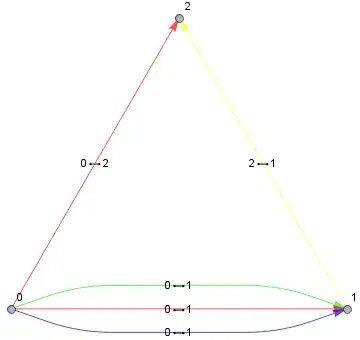
I have the following edgelist and colors:

edges = {0 <-> 1, 0 <-> 2, 0 <-> 1, 2 <-> 1, 0 <-> 1};
colors = {Blue, Red, Red, Yellow, Green};

But I can't find a way to color the edges using these colors. My first try of course was to use something like:

Graph[edges, EdgeStyle -> {0 <-> 1 -> Blue,  0 <-> 2 -> Red, 0 <-> 1 -> Red, 
  2 <-> 1 -> Yellow, 0 <-> 1 -> Green}]

But in this all of the edges between 0 and 1 turn out to be green even though only one of them should be. I also tried to do this with 

colors = {Blue, Red, Red, Yellow, Green};
i = 1;
Graph[{0 <-> 1, 0 <-> 2,  0 <-> 1, 2 <-> 1,  0 <-> 1}, 
EdgeShapeFunction -> ({Arrowheads[Large], Thick, colors[[i++]], 
 Arrow @ #} &)]

But now a wrong edge gets the green color for some reason. Any ideas? I already looked into Graph: Coloring parallel edges individually which didn't help me with this really.

kglr
  • 394,356
  • 18
  • 477
  • 896
NPHA
  • 135
  • 5
  • 1
    Mathematica does not properly support edge properties for multigraphs. It is not possible to assign a separate EdgeStyle property to different edges that run between the same vertices. If you care about this functionality, you should contact Wolfram Support and request it. I believe they will only fix this if many people request it. – Szabolcs Oct 19 '18 at 13:26
  • @Szabolcs Really? That's a shame for me at least. – NPHA Oct 19 '18 at 14:07
  • See here: https://mathematica.stackexchange.com/q/92014/12 EdgeWeight, EdgeCapacity and EdgeCost are the only properties that work for multigraphs (if you're careful). Unfortunately, this limitation is not properly documented, things just fail ... However, development of Graph has just picked up again (there was a recent Twitch streams about it), so it's the best time to request this feature again. If you believe you need this, please do write to Wolfram Support and request it. – Szabolcs Oct 19 '18 at 14:22
  • @Szabolcs Sure, will do! But couldn't I go around it then and define different weights or costs to edges and then color them according to the weight/cost? Or will it still fail? – NPHA Oct 19 '18 at 14:29
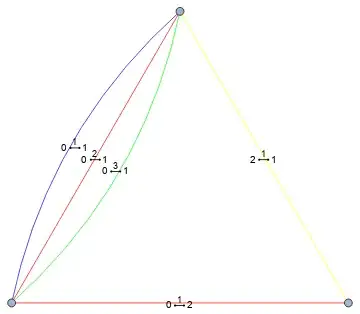
  • The issue is that EdgeStyle cannot be used. Since Mathematica refers to edges by their endpoints, there is no way to distinguish between parallel edges, and assign different properties to them. Colouring is normally done through EdgeStyle. That won't work here. Thus any solution one might come up with will be inconvenient and error-prone. – Szabolcs Oct 19 '18 at 14:34
  • The solution I was aware of, and the one you also found, was to define a new EdgeRenderingFunction, and colour edges with different colours on the 1st, 2nd, etc. calls of this function. However, as you just discovered, the EdgeRenderingFunction is not called in the same order as edges appear in EdgeList. I guess you could record the order in which edges are rendered, then reorder the colors vector based on that. But this is hackish and error prone again. – Szabolcs Oct 19 '18 at 14:36
  • EdgeWeight, etc. won't help here because it can't colour things. Only EdgeStyle (or EdgeRenderingFunction) can colour things. Mathematica has no built-in feature to directly map an EdgeWeight into an EdgeStyle in some way. My IGraph/M package does have such a feature, but it will protect you by detecting multigraphs and reporting an error. Obviously, I can't implement a robust mapping between edge properties on a multigraph until Wolfram starts supporting these properly. – Szabolcs Oct 19 '18 at 14:38
  • @Szabolcs Oh, I see. Anyways your comments have been useful as I think I learned important things about Mathematica once again. – NPHA Oct 19 '18 at 14:40
  • I hope you're not scared away from Mathematica's Graph for good. Do check out IGraph/M if you work with graphs. Feel free to email me with any feedback. – Szabolcs Oct 19 '18 at 14:42
  • @Szabolcs Any tips how you can record the order in EdgeRenderingFunction? This would be useful also in other cases than hacking this thing. – NPHA Oct 19 '18 at 14:42
  • @Szabolcs I have been using it in multiple occasions but this is the first time I'm really having any issues (as this is the first project I need multigraphs for). So don't fear, not leaving it for good :) – NPHA Oct 19 '18 at 14:44
  • The edge rendering function takes the edge name as its 2nd argument. You can Sow it, then Reap it. You get an edge list this way. Now find a permutation that transforms this edge list to the EdgeList of the graph (or vice versa). This can be done with Ordering. Note that Ordering can also be used to invert a permutation—this will be useful for this task. – Szabolcs Oct 19 '18 at 14:54
  • @Szabolcs I made it work, thank you. However as you said it's error prone. Still as I only needed a visualization of one specific graph it's good for that. – NPHA Oct 19 '18 at 15:51

1 Answers1

5
edges = {0 \[UndirectedEdge] 1, 0 \[UndirectedEdge] 2,  
  0 \[UndirectedEdge] 1, 2 \[UndirectedEdge] 1,  0 \[UndirectedEdge] 1};
colors = {Blue, Red, Red, Yellow, Green};
styles = GroupBy[Thread[edges -> colors], First -> Last]

enter image description here

esf = {First[styles[#2] = RotateRight[styles[#2]]], Arrow[#]} &;

Graph[edges, EdgeStyle -> Normal[styles], EdgeShapeFunction -> esf, 
 VertexLabels -> "Name", EdgeLabels -> "Name" ]

enter image description here

Update: In version 12.1 you can use EdgeTaggedGraph to have individual styles and labels for multi-edges:

stylededges = MapThread[Style, {edges, colors}];
EdgeTaggedGraph[stylededges, EdgeLabels -> "Name" ]

enter image description here

kglr
  • 394,356
  • 18
  • 477
  • 896