Computing the Lyuponov exponent for the Duffing system

Question

Does anyone know (simple) Mathematica code for computing the Lyuponov exponent for the Duffing system?

x''[t] + 0.15 x'[t] - x[t] + x[t]^3== 7*Cos[t]
{x[0] == 0, x'[0] == 0}

The system is in chaotic state but I got negative values for Lyapunov Exponents by using the suggested methods I am not sure what is wrong — Kaleed Ad, Nov 05 '18 at 17:48
P.S., welcome to Mathematica.SE! I suggest the following:

As you receive help, try to give it too, by answering questions in your area of expertise.

Take the [tour] and check the faqs!

When you see good questions and answers, vote them up by clicking the gray triangles, because the credibility of the system is based on the reputation gained by users sharing their knowledge.

Also, please remember to accept the answer, if any, that solves your problem, by clicking the checkmark sign! — Chris K, Nov 05 '18 at 18:21

score 5 · Accepted Answer · answered Nov 06 '18 at 18:41

5

My previous code for LyapunovExponents from this answer did not handle non-autonomous systems like this properly. Thanks for pointing that out! I've updated it to fix this mistake and it seems to work now.

Putting your system in first-order form:

eqns = {x'[t] == y[t], y'[t] == -0.15 y[t] + x[t] - x[t]^3 + 7 Cos[t]};

Then calculating Lyapunov exponents:

LyapunovExponents[eqns, {x -> 0, y -> 0}, ShowPlot -> True]

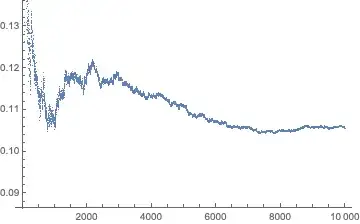
Mathematica graphics

(* {0.10542, -0.25542} *)

answered Nov 06 '18 at 18:41

Chris K

20,207
3
39
74

1

I used your code after your modification and I was able to get very close results for this work https://arxiv.org/pdf/physics/0303077.pdf for this eq: eqns = {x'[t] == y[t], y'[t] == 2.5*Sin[t] - 0.1 y[t] - Sin[x[t]]}; This is what I got {0.160632, -0.260632} And this what they got {0.160 , −0.262} That is very good By the way, should I always use the initial conditions for LyapunovExponents[eqns, {x -> 0, y -> 0}, ShowPlot -> True]
or the value for x and y at any time is fine? Thanks you
– Kaleed Ad Nov 06 '18 at 19:27
Great, thanks for the link. You can use whatever initial conditions (t=0) you want. – Chris K Nov 06 '18 at 20:22

Computing the Lyuponov exponent for the Duffing system

1 Answers1

Linked