Find Root doesn't work properly

Question

I use a FindRoot that doesn't find the right solution in some range, the FindRoot is the following:

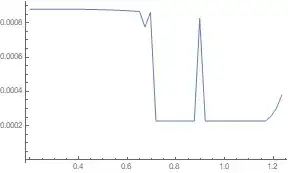
tabexp = ParallelTable[{Temp,V /.FindRoot[Ifix - Isis[V/2, 0.2, Temp, 1.5, 1.4, \[Gamma]0, \[Gamma]0,RSISIS], {V, 4.05 d0Al[1.5]/q, 1. d0Al[1.5]/q,4.1 d0Al[1.5]/q}, AccuracyGoal -> 25,  PrecisionGoal -> 25,MaxIterations -> 2000]}, {Temp, 0.2, 1.25, 0.9/40}];

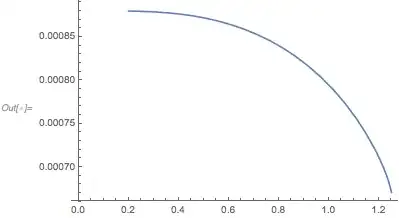
This is the plot of the FindRoot output tabexp:

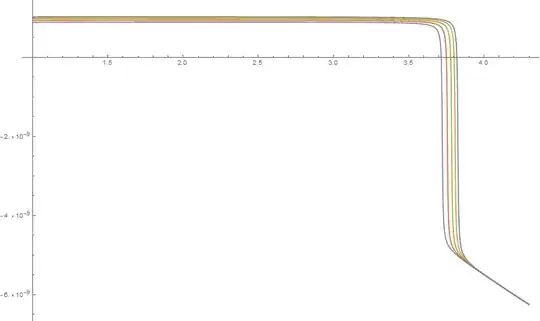
The point is that the graphical solution is easy:

Plot[Evaluate[Table[{Ifix -Isis[V/2 d0Al[1.5]/q, 0.2, Tx, 1.5, 1.4,[Gamma]0, \[Gamma]0,RSISIS]}, {Tx, 0.6, 0.8, 0.05}]], {V, 1 , 4.3},PlotRange -> All]

I don't understand why it's not working properly. If you need all the code it is the following:

q = 1.602176487` 10^-19;
kB = 1.3806504` 10^-23;
\[HBar] = 1.054571628251774` 10^-34;
TcAluminio = 1.55;
d0Al[TcAl_] := 1.764 kB TcAl;
d0max = 1.764 kB 1.65;
delta[T_] := Tanh[1.74 Sqrt[1/T - 1]];
\[CapitalDelta]Al[T_, TcAl_] := delta[T/TcAl] d0Al[TcAl];

ngammaAl[energy_, T_, gamma_, TcAl_] := 
  Abs[Re[(energy + I gamma d0Al[TcAl])/
    Sqrt[(energy + I gamma d0Al[TcAl])^2 - \[CapitalDelta]Al[T, 
      TcAl]^2]]];
Isis[V_, T1_, T2_, TcAlP_, TcAlI_, gamma1_, gamma2_, Rjunction_] := 
  Re[1/(    q Rjunction)
     NIntegrate[
     ngammaAl[energy - q V, T1, gamma1, TcAlP] ngammaAl[energy, T2, 
       gamma2, 
       TcAlI] (1/(Exp[(energy - q V)/(kB T1)] + 1) - 1/(
        Exp[energy/(kB T2)] + 
         1)), {energy, -10 d0max, -\[CapitalDelta]Al[T1, 
        TcAlP], \[CapitalDelta]Al[T2, TcAlI], \[CapitalDelta]Al[T2, 
       TcAlI], \[CapitalDelta]Al[T1, TcAlP], 10 d0max}, 
     MinRecursion -> 4, 
     Method -> {"GlobalAdaptive", "MaxErrorIncreases" -> 100000, 
       "SymbolicProcessing" -> 0, "SingularityHandler" -> None}, 
     PrecisionGoal -> 5]];
\[Gamma]0 = 10^-3;
RSISIS = 55000;
Ifix = Isis[0.0006/2, 1.1, 1.1, 1.5, 1.4, \[Gamma]0, \[Gamma]0, 
  RSISIS]

Thanks in advance and sorry for the bad English.

Probably not a good sign when I evaluate your code and it spews a notebook's worth of error messages at me. — ktm, Nov 07 '18 at 14:04
Maybe you're right, and the problem is related to the warning. However I always work like this. The plot doesn't generate any errors, they all come from the find root. In particular, the option ''oscillatory'' seems to generate many warnings, although it usually gives the best result. — Giuliano-Francesco TIMOSSI, Nov 07 '18 at 14:11

score 2 · Accepted Answer · answered Nov 07 '18 at 20:04

2

V_?NumericQ removes some errors. WorkingPrecision -> 32 removes others. NDSolve tracks the solution.

ClearAll[Isis];
Isis[V_?NumericQ, T1_, T2_, TcAlP_, TcAlI_, 
   gamma1_, gamma2_, Rjunction_] := Re[1/(q Rjunction) NIntegrate[
     SetPrecision[
      ngammaAl[energy - q V, T1, gamma1, TcAlP] ngammaAl[energy, T2, 
        gamma2, TcAlI] (1/(Exp[(energy - q V)/(kB T1)] + 1) - 
         1/(Exp[energy/(kB T2)] + 1)),
      50], {energy, -10 d0max, -ΔAl[T1, TcAlP], ΔAl[T2, TcAlI], ΔAl[T2, 
       TcAlI], ΔAl[T1, TcAlP], 10 d0max}, 
     MinRecursion -> 4, 
     Method -> {"GlobalAdaptive", "MaxErrorIncreases" -> 100000, 
       "SymbolicProcessing" -> 0, "SingularityHandler" -> None}, 
     PrecisionGoal -> 5, WorkingPrecision -> 32]];

sol = NDSolve[{Ifix == 
    Isis[V[Temp]/2, 0.2, Temp, 1.5, 1.4, γ0, γ0, 
     RSISIS], x'[Temp] == 1, x[0.2] == 0.2,
   V[0.2] == (VV /. 
      FindRoot[
       Ifix - Isis[VV/2, 0.2, 0.2, 1.5, 1.4, γ0, γ0, 
         RSISIS], {VV, 4.05 d0Al[1.5]/q, 3. d0Al[1.5]/q, 
        4.1 d0Al[1.5]/q}])},
  V,
  {Temp, 0.2, 1.25}]

ListLinePlot[V /. First@sol]

answered Nov 07 '18 at 20:04

Michael E2

235,386
17
334
747

Thank you this is a very good solution! I was using the find root to create a table which I was interpolating to fit some data, is it possible to implement your code to create a function of more variable? I mean now sol=sol[Temp], I would like to create a function like sol=sol[Temp,gamma0,Rsisis...]. – Giuliano-Francesco TIMOSSI Nov 08 '18 at 11:17
@Giuliano-FrancescoTIMOSSI In theory, yes. In practice, it might be difficult. Methods for multivariate interpolation and multivariate differential equations (PDEs) are not as robust as single variable methods. I'm fairly confident that if the computations are not numerically ill-conditioned, it can be done in some way, but it might not be a simple adaptation. – Michael E2 Nov 08 '18 at 11:27
Thanks a lot for the answer. We are not use to use the NDSolve and we are wondering about the x variable. Why do you put it there? Sorry. Anyway thanks a lot! – Giuliano-Francesco TIMOSSI Nov 08 '18 at 15:06
@Giuliano-FrancescoTIMOSSI The x variable is a dummy variable used to turn your equation into a DAE system. NDSolve steps Temp from 0.2 to 1.25, integrating x[Temp] and using FindRoot to solve for V[Temp] at each step. It returns the table of values computed in the form of an InterpolatingFunction. Is there some reason you're not allowed to use NDSolve? Is it a homework problem? The advantage is NDSolve automatically figures out the starting point for FindRoot at each step. – Michael E2 Nov 09 '18 at 16:11
I can use it no problem sadly i never follow any course and I was just wondering on how to use the NDsolve in the proper way in the future. NDSolve seams to be much more efficient than my way to proceed. – Giuliano-Francesco TIMOSSI Nov 19 '18 at 17:17

Find Root doesn't work properly

1 Answers1

Linked