Roots of a polynomial

Question

In Mathematica I have represented the following polynomial $a x^4 + b x^2 + c x+2$ using the Plot command and, through the Manipulate command, it is possible to vary the parameters $a$, $b$, $c$. Now, however, I would like the program to give me back the roots of the polynomial according to the parameters $a$, $b$, $c$ .... could you help me kindly?

This is the code:

Manipulate[
  Plot[a*x^4 + b*x^2 + c*x + 2, {x, -20, 20}, PlotRange -> {{-20, 20},{-20, 20}}]
  ,{a,-1, 1}
  ,{b,-10, 10}
  ,{c,-10, 10}
  ,ControlPlacement -> Right
]

Maybe some variant of roots[a_, b_, c_] := x /. Solve[a*x^4 + b*x^2 + c*x + 2 == 0, x] — Daniel Lichtblau, Dec 04 '18 at 20:09
Take a look at this post Factoring a two variable polynomial in a special way. If you examine it, you should be able to solve your problem. — Artes, Dec 04 '18 at 20:12

score 4 · Answer 1 · answered Dec 05 '18 at 16:02

As Dan Lichtblau has already commented you can use

Solve[a*x^4 + b*x^2 + c*x + 2 == 0, x]

to obtain the roots. But I suspect that you really, really, really don't want to do this. Why?

A long time ago, (in The Mathematica Journal 9(3)), Daniel explained why you should use Root instead, e.g. via Solve[a*x^4 + b*x^2 + c*x + 2 == 0, x, Quartics -> False]

The Root form is a concise way of expressing algebraic numbers via the minimal polynomial they satisfy, along with a canonical ordering in the complex plane (specified by the second argument of Root).
To get a radical form, you can use ToRadicals. Clearly, this output is more complicated than the Root form.

In addition to size, there are other reasons to prefer the Root form:

It is faster to obtain.
It is numerically more stable to evaluate. In general, radical formulations are prone to numeric problems. Root objects do not have this liability.
When the roots of an irreducible cubic are all real but not rational, the so-called casus irreducibilus shows that they still must be expressed in terms of I. This means that numeric evaluation will give small imaginary parts unless, by happenstance, they exactly cancel. Small numeric error from round-off makes this unlikely.
For sufficiently complicated algebraics, it is often faster to evaluate the Root form numerically, at least at high precision.
Polynomial combinations of Root objects simplify using RootSum and RootReduce.
Derivatives of Root objects with respect to a parameter are expressed in terms of Root objects. This is useful for (eigenvalue) sensitivity analysis.

So, for all practical computation, you are better off working with Root objects.

Bob Hanlon · Answer 2 · 2018-12-05T20:02:05.520

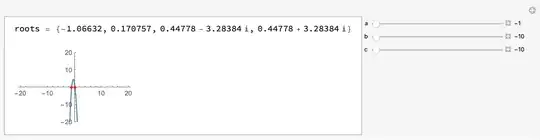
Manipulate[
 Column[{
   StringForm["roots = ``",
    roots = x /. NSolve[a*x^4 + b*x^2 + c*x + 2 == 0, x]],
   Spacer[5],
   Plot[a*x^4 + b*x^2 + c*x + 2, {x, -20, 20},
    PlotRange -> 20,
    Epilog -> {Red, AbsolutePointSize[4], 
      Tooltip[Point[{#, 0}], #] & /@ Cases[roots, _Real]}]}],
 {a, -1, 1, 0.02, Appearance -> "Labeled"},
 {b, -10, 10, 0.2, Appearance -> "Labeled"},
 {c, -10, 10, 0.2, Appearance -> "Labeled"},
 ControlPlacement -> Right]

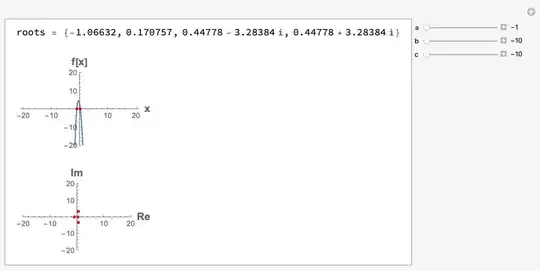
EDIT: If you also wish to see the roots in the complex plane

Manipulate[
 Column[{
   StringForm["roots = ``",
    roots = x /. NSolve[a*x^4 + b*x^2 + c*x + 2 == 0, x]],
   Spacer[5],
   Plot[a*x^4 + b*x^2 + c*x + 2, {x, -20, 20},
    PlotRange -> 20,
    AxesLabel -> (Style[#, 14, Bold] & /@ {"x", "f[x]"}),
    Epilog -> {Red, AbsolutePointSize[4], 
      Tooltip[Point[{#, 0}], #] & /@ Cases[roots, _Real]}],
   Spacer[5],
   ListPlot[Tooltip /@ ReIm /@ roots,
    PlotStyle -> Directive[Red, AbsolutePointSize[4]],
    PlotRange -> {{-20, 20}, {-20, 20}},
    AxesLabel -> (Style[#, 14, Bold] & /@ {Re, Im})]}],
 {a, -1, 1, 0.02, Appearance -> "Labeled", ImageSize -> Small},
 {b, -10, 10, 0.2, Appearance -> "Labeled", ImageSize -> Small},
 {c, -10, 10, 0.2, Appearance -> "Labeled", ImageSize -> Small},
 ControlPlacement -> Right]

Roots of a polynomial

2 Answers2