Factoring a two variable polynomial in a special way

Question

Let $$f=x^9-x^6+4x^5y+2x^3y^2-y^4$$ I would like to factorize $f$ into form: $$(y-F_1(x))\cdots(y-F_k(x))$$ over complex numbers. How can I do it with Mathematica?

Answer 1

Since we can consider $f$ as a $4-$th order polynomial (with respect to $y$) we can always factorize it as you claim in terms of radicals, but for the sake of simplicity let's start writing it symbolically in terms of the Root objects defining $f$ to be p[x,y]:

p[x_, y_] := x^9 - x^6 + 4 x^5 y + 2 x^3 y^2 - y^4

pf[x_, y_] = -Times @@ (y - (y /. {ToRules @ Reduce[p[x, y] == 0, {x, y}]}))

-((y - Root[x^6 - x^9 - 4 x^5 #1 - 2 x^3 #1^2 + #1^4 &, 1]) 
  (y - Root[x^6 - x^9 - 4 x^5 #1 - 2 x^3 #1^2 + #1^4 &, 2]) 
  (y - Root[x^6 - x^9 - 4 x^5 #1 - 2 x^3 #1^2 + #1^4 &, 3]) 
  (y - Root[x^6 - x^9 - 4 x^5 #1 - 2 x^3 #1^2 + #1^4 &, 4]))

We can simplify this form to its original form:

% // Simplify
% == p[x, y]

-x^6 + x^9 + 4 x^5 y + 2 x^3 y^2 - y^4
True

We can use the above factorized form pf[x,y] consequently in computations. It might be advantageous to observe how the roots depend on the x parameter with the following animation:

anim = 
  Table[
    GraphicsRow[ 
      Table[ 
        ContourPlot[ g[ p[x, u + I w]], {u, -10, 10}, {w, -10, 10}, 
          Epilog -> {Blue, PointSize[0.03], Point[ Table[
            {Re @ #, Im @ #}& @ Root[x^6 - x^9 - 4 x^5 #1 - 2 x^3 #1^2 + #1^4 &, m], 
            {m, 4}]]}, 
          ColorFunction -> "StarryNightColors", ImageSize -> 400], 
        {g, {Re, Im}}]], 
    {x, -2.5, 2.5, 0.1}];

ListAnimate[ anim, Paneled -> False]

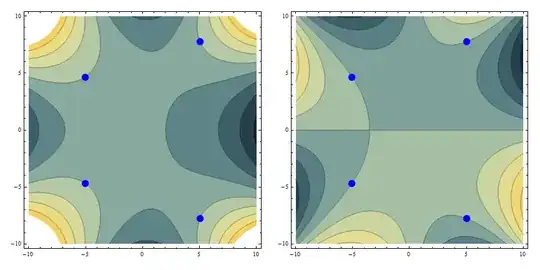
Alternatively we could exploit the Quartics -> False option of Solve (mind we have used only y as a variable, otherwise we would get a warning):

-Times @@ (y - (y /. Solve[ p[x, y] == 0, y, Quartics -> False]))

It's traditional form in terms of radicals is slightly involved:

ToRadicals[ -pf[x, y]] // TraditionalForm

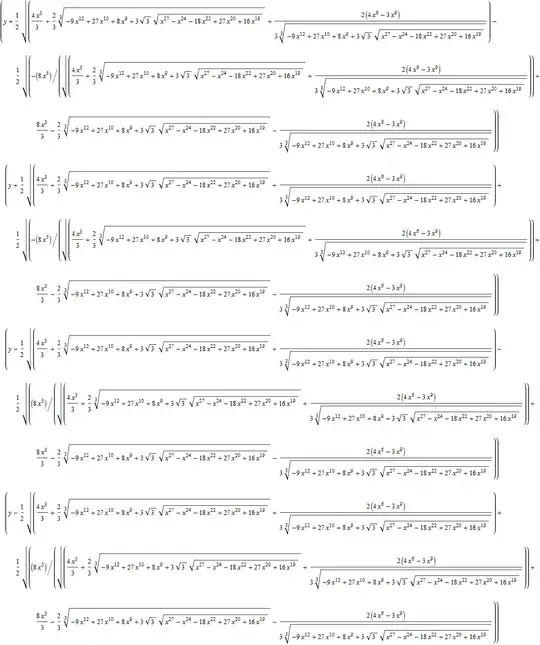
This is the reason why we need sometimes options like Quartics or Cubics. For more information on roots see e.g. How do I work with Root objects?, how you could exploit Factor: Factoring polynomials to factors involving complex coefficients.