A numerical boundary conditions paradox

Question

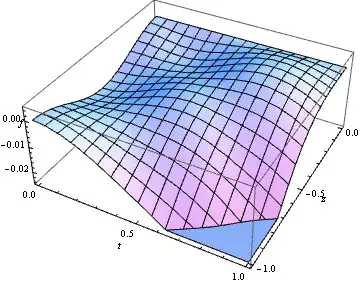
For $(t,z)\in[0,1]\times[-1,0]$

zmin = -1; tmax = 1;

and some fields $w(t,z)$ and $y(t,z)$

n = 100; h = -zmin/(n-1);
W[t_] = Table[w[i][t], {i, n}]; 
Y[t_] = Table[y[i][t], {i, n}];

let there be the following PDE's system $$\partial_tw=\partial_zy+w\partial_zw$$ $$\partial_ty=\partial_zw+w\partial_zy$$

For the implementation of the Method of Lines derivatives $\partial_zw$ and $\partial_zy$ are numerically approximated as

Wz[t_] = Join[{(w[2][t] - w[1][t])/h}, 
Table[(w[i + 1][t] - w[i - 1][t])/(2h), {i, 2, n - 1}], {(
w[n][t] - w[n - 1][t])/h}];

and

Yz[t_] = Join[{(y[2][t] - y[1][t])/h}, 
Table[(y[i + 1][t] - y[i - 1][t])/(2h), {i, 2, n - 1}], {(
y[n][t] - y[n - 1][t])/h}];

Notice that the above derivative formulas change for $i=1$ (i.e. $z=-1$) and $i=100$ (i.e. $z=0$). This is a way to handle the fact that numerical integration for $z$ is confined in $[-1,0]$ and does not imply any boundary condition.

Then the above PDE's system can be written as

wall[t_] = Yz[t] + W[t]*Wz[t];
eqw = Thread[
D[W[t], t] == wall[t] - PadLeft[{ wall[t][[n]]}, n]];
eqy = Thread[D[Y[t], t] == Wz[t] + W[t]*Yz[t]];

The only boundary condition that is implied by the above equations is that $$w(t,0)=0$$ and this is the reason for the cumbersome statement of the dynamical equation for $w$ ( further explanation: press ctrl+F and type "here is the answer for point 3").

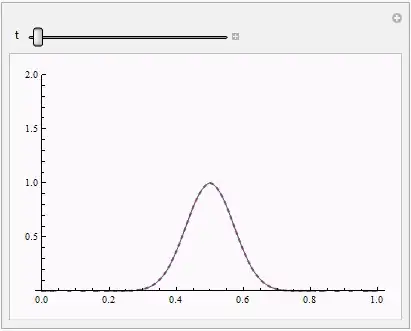
The boundary condition is accompanied by the following initial conditions

w0[z_] = -0.01*Sin[z*Pi]^2;
y0[z_] = 1;
initw = Thread[W[0] == Table[w0[zmin + (i-1)*h], {i, n}]];
inity = Thread[Y[0] == Table[y0[zmin + (i-1)*h], {i, n}]];

and then NDSolve is called to implement the method of lines

lines = NDSolveValue[{eqw, eqy, initw, inity}, {W[t], Y[t]}, {t, 0, 
tmax}];

So there arise the following questions:

Except $w(t,0)=0$ is there any other boundary condition implicit in the finite difference equations? If it does then which? If it doesn't then why does the code run? The problem seems underdetermined.
Can one call the Method of Lines as internal routine so as to increase the accuracy of the above code?

I am working on these but would appreciate any help.

I believe that boundary conditions are needed for both w and y. I am unaware of any way to call Method of Lines as internal routine, but you could use NDSolve directly to solve the coupled PDEs. — bbgodfrey, Dec 23 '18 at 13:36
@xzczd here is the answer for point 3. PadLeft[{ wall[t][[n]]}, n] creates a list with n elements all of which is zero except the nth one that equals wall[t][[n]] . As a result the subtraction results in a list of n elements the first n-1 equal to Yz[t] + W[t]*Wz[t] and the last one equal to zero. This means that $\partial_tw(t,0)=0$ and results in $w(t,0)=w(0,0)=\sin(0)^2=0$. — dkstack, Dec 23 '18 at 13:36
@bbgodfrey boundary condition about y concerns its value or could be stated in terms of its z-derivative? Also can you see why the code runs I mean if there is an implicit boundary condition in my code? — dkstack, Dec 23 '18 at 13:50
@xzczd concerning point 1. the choice h=-zmin/n results in a $z$-grid of $n$ points the $i=1$ point being $z=zmin+h$ and the $i=n$ point being $z=0$. So spatial integration is done for $z\in[-1+h,0]$ and not $[-1,0]$. I think this is not essential to the question but I will fix the code as soon as possible. — dkstack, Dec 23 '18 at 14:02
Oh… as to point3, you're right, I forgot about the i.c., but I think it's better to explain this a bit in the question. @bbgodfrey Have you read this post?: https://scicomp.stackexchange.com/q/28033/5331 — xzczd, Dec 23 '18 at 14:20
@xzczd what do you think of point 1.? I mean is there any difference between h = -zmin/n and h = -zmin/(n-1) other than adding $h$ to the left end of $[-1,0]$? — dkstack, Dec 23 '18 at 14:25
There won't be any obvious difference when the grid is dense enough, of course. But it's just better to avoid this inaccuracy. — xzczd, Dec 23 '18 at 14:48

xzczd · Answer 1 · 2018-12-25T14:31:41.537

The solution you've observed is the artifact of 1st order one-sided difference formula

$$f' (x_n)\simeq \frac{- f (x_{n}-h)+ f (x_n)}{ h}$$

for approximating the PDE at the boundary. This can be confirmed by replacing it with 2nd order one-sided formula

$$f' (x_n)\simeq \frac{f (x_{n}-2h)-4 f (x_{n}-h)+3 f (x_n)}{2 h}$$

If you're not familiar with one-sided formula, start from page 6 of this book.

zmin = -1; tmax = 1;

n = 100; h = -zmin/(n - 1);
W[t_] = Table[w[i][t], {i, n}]; 
Y[t_] = Table[y[i][t], {i, n}];


help[var_] := With[{w = var}, Join[{-{1, -4, 3}.{w[3][t], w[2][t], w[1][t]}/(2 h)}, 
   Table[(w[i + 1][t] - w[i - 1][t])/(2 h), {i, 2, 
     n - 1}], {{1, -4, 3}.{w[n - 2][t], w[n - 1][t], w[n][t]}/(2 h)}]]

Wz[t_] = help@w ;
Yz[t_] = help@y;


wall[t_] = Yz[t] + W[t]*Wz[t];
eqw = Thread[
   D[W[t], t] == wall[t] - PadLeft[{ wall[t][[n]]}, n]];
eqy = Thread[D[Y[t], t] == Wz[t] + W[t]*Yz[t]]; 

w0[z_] = -0.01 Sin[z π]^2;
y0[z_] = 1;
initw = Thread[W[0] == Table[w0[zmin + (i - 1)*h], {i, n}]];
inity = Thread[Y[0] == Table[y0[zmin + (i - 1)*h], {i, n}]];

lines = NDSolveValue[{eqw, eqy, initw, inity}, {W[t], Y[t]}, {t, 0, 
    tmax}];

{testw, testy} = 
 ListInterpolation[
    Developer`ToPackedArray@#[[0]]["ValuesOnGrid"] & /@ # // 
     Transpose, {#[[1, 0]]["Coordinates"][[1]], Array[# &, n, {zmin, 0}]}] & /@ lines

Plot3D[testw[t, z], {t, 0, tmax}, {z, zmin, 0}, AxesLabel -> {t, z, f}]

Mathematica graphics

But if we use 1st order one-sided formula instead:

help[var_] := With[{w = var}, Join[{(w[2][t] - w[1][t])/h}, 
   Table[(w[i + 1][t] - w[i - 1][t])/(2 h), {i, 2, n - 1}], {(
      w[n][t] - w[n - 1][t])/h}]]

The solution will be

Mathematica graphics

The difference is obvious i.e. the solution depends on how we approximate the differential term at the boundary!

Further check by varying n shows both solutions are stable. This behavior never shows up when b.c. is enough AFAIK. For example, when dealing with the initial-boundary value problem

tend = 1/10; xl = 0; xr = 1;
With[{u = u[t, x]}, eq = D[u, t] == D[u, x, x];
 ic = u == Exp[-100 (x - (xl + xr)/2)^2] /. t -> 0;
 bc = {u == 0 /. x -> xl, D[u, x] == 0 /. x -> xr};]

sol = NDSolveValue[{eq, ic, bc}, u, {t, 0, tend}, {x, xl, xr}]

Both 1st and 2nd order approximation for the b.c. lead to the same solution, when the grid is dense enough:

Clear@dx
formula = eq /. {D[u[t, x], t] -> u[x]'[t], 
    D[u[t, x], x, x] -> (u[x - dx][t] - 2 u[x][t] + u[x + dx][t])/dx^2};

points = 25;
dx = (xr - xl)/(points - 1);
ode = Table[formula, {x, xl + dx, xr - dx, dx}];
odeic = Table[ic /. u[t_, x_] :> u[x][t] // Evaluate, {x, xl, xr, dx}];

bcnew1 = bc[[1]] /. u[t_, x_] :> u[x][t];

bcnew2 = bc[[2]] /. 
   D[u[t, x_], x_] :> (u[x - 2 dx][t] - 4 u[x - dx][t] + 3 u[x][t])/(2 dx);
bcnew3 = bc[[2]] /. D[u[t, x_], x_] :> (- u[x - dx][t] + u[x][t])/(dx);
mid[bc_] := (sollst = 
   NDSolveValue[{ode, odeic, bcnew1, bc}, 
    u /@ Array[# &, points, {xl, xr}], {t, 0, tend}];
  ListInterpolation[
     Developer`ToPackedArray@#["ValuesOnGrid"] & /@ # // 
      Transpose, {#[[1]]["Coordinates"][[1]], Array[# &, points, {xl, xr}]}] &@sollst)
soltest1 = mid[bcnew2];
soltest2 = mid[bcnew3];
Manipulate[Plot[{soltest1[t, x], soltest2[t, x]}, {x, xl, xr}, 
  PlotStyle -> {Automatic, {Thick, Dashed}}, PlotRange -> {0, 2}], {t, 0, tend}]

OK, then how to explain this behavior? Is the difference formula actually equivalent to a hidden b.c.? This is exactly what I've asked in this and this post, but sadly nobody has found a satisfactory answer so far.

xzczd, what do you think of this post? It may lead to a general method for first order IBVP problems that mix spatial and temporal derivatives. — dkstack, Jan 17 '19 at 16:31

dkstack · Answer 2 · 2018-12-26T14:21:21.240

0

@bbgodfrey commented above that boundary conditions (b.c.) are needed for both $y$ and $w$. These b.c. can be time-independent, i.e. of the form $y_b=const.$ and $w_b=const.$ But it is reasonable that b.c. could be time-independent as well, i.e. of the form $y_b=y_b(t)$ and $w_b=w_b(t)$. Fuctions $y_b(t)$ and $w_b(t)$ can have an analytic expression, but it is conceivable that this won't be always the case. They could be solutions of some differential equation that does not have any analytic solution. And in particular, I think here comes the answer, functions $y_b(t)$ and $w_b(t)$ could be solutions of the given PDE system.

In short I think that the code I posted gives a solution that by construction is characterised by b.c. $y(t,-1), y(t,0), w(t,-1)$ that are solutions of the PDE's system in question. These are complemented by b.c. $w(t,0)=0$ and together with initial conditions (i.c.) lead to a unique solution-the one to which 1st and 2nd order approximation mentioned by @xzczd converge as grid density increases.

I am not a methematician so I cannot be entirely sure that my answer is correct,though apparently reasonable. An expert's confirmation would be important.

Also if the answer is correct here comes the question if one can call method of lines as an internal routine and therefore avoid explicit discretization of the problem.

edited Dec 26 '18 at 14:21

answered Dec 26 '18 at 14:02

dkstack

103
6

"In short I think that the code I posted gives a solution that by construction is characterised by b.c. $y(t,-1), y(t,0), w(t,-1)$ that are solutions of the PDE's system in question." Notice that given the highest differential order of $w$ and $y$ respect to $z$ is $1$, usually you only need $2$ boundary conditions. (Related: https://math.stackexchange.com/q/450367/58219) There exist more involved cases e.g. Inviscid Burgers equation though. – xzczd Dec 26 '18 at 14:29
Ok then forget about $y(t,-1)$ and $ w(t,-1)$. My point is that the solution that occurs is not an artifact but a fare and square solution with b.c. that are time dependent, without any analytic expression, and which by construction are numerical solutions of the above PDE system. – dkstack Dec 26 '18 at 14:34
Notice I've never denied that lines etc. are solutions for the PDE. I use the word "artifact" because those solutions aren't determined before a certain one-sided formula is chosen. – xzczd Dec 26 '18 at 15:10
Yes but you have proven that any one-sided formula in the limit of very dense grid points to the same solution. – dkstack Dec 26 '18 at 15:53
So we can reverse our logic and say: yes b.c. can be time dependent. Yes time dependent b.c. may be solutions of equations that do not have analytical solutions. And yes time dependent b.c. can be solutions of the specific PDE system we try to solve. – dkstack Dec 26 '18 at 15:56
And then ask: how can we tell mathematica to integrate under such b.c.? – dkstack Dec 26 '18 at 15:57
Simple answer: using the one sided derivative formula. Ask: which formula should I use? Say: All formulas point to the same answer in the limit of continuous grid. – dkstack Dec 26 '18 at 16:00
The solution thus obtained is not trivial nor artificial. Is a certain solution with certain b.c. – dkstack Dec 26 '18 at 16:01
"Yes but you have proven that any one-sided formula in the limit of very dense grid points to the same solution. " Only if the b.c. is enough. When b.c. is not enough like in your case, different one-sided formula leads to different solution. – xzczd Dec 26 '18 at 16:36

A numerical boundary conditions paradox

2 Answers2

Linked