The following PDE's-system-solving code
cn = 10^-1; zmin = -1*cn; tmax = 1*cn;
IBVP = NDSolve[{D[w[t, z], t] ==
D[q[t, z], z] + w[t, z]*D[w[t, z], z],
D[q[t, z], t] == D[w[t, z], z] + w[t, z]*D[q[t, z], z],
w[0, z] == 0, w[t, 0] == 0, q[0, z] == 1,
q[t, 0] == Cos[t]^2}, {w, q}, {t, 0, tmax}, {z, 0, zmin},
Method -> {"MethodOfLines",
"SpatialDiscretization" -> {"TensorProductGrid",
"MinPoints" -> 80, "MaxPoints" -> 100}}];
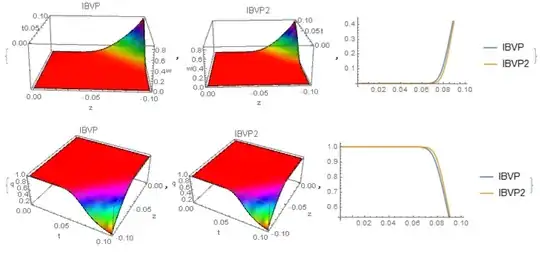
Plot3D[w[t, z] /. IBVP, {t, 0, tmax}, {z, 0, zmin}]
is just fine for Mathematica. However when the PDE $$\partial_zB(t,z)=0$$ is added to the system along with trivial initial-boundary conditions $$B(0,z)=0\qquad B(t,0)=0$$ i.e. the code becomes
cn = 10^-1; zmin = -1*cn; tmax = 1*cn;
IBVP2 = NDSolve[{D[w[t, z], t] ==
D[q[t, z], z] + w[t, z]*D[w[t, z], z],
D[q[t, z], t] == D[w[t, z], z] + w[t, z]*D[q[t, z], z],
D[B[t, z], z] == 0, w[0, z] == 0, w[t, 0] == 0, q[0, z] == 1,
q[t, 0] == Cos[t]^2, B[0, z] == 0, B[t, 0] == 0}, {w, q, B}, {t,
0, tmax}, {z, 0, zmin},
Method -> {"MethodOfLines",
"SpatialDiscretization" -> {"TensorProductGrid",
"MinPoints" -> 80, "MaxPoints" -> 100}}];
Plot3D[w[t, z] /. IBVP2, {t, 0, tmax}, {z, 0, zmin}]
Mathematica displays the following error
Warning: an insufficient number of boundary conditions have been specified for the direction of independent variable z. Artificial boundary effects may be present in the solution. >>
It is conceivable that one can solve the IBVP for $B(t,z)$ seperately and get $B(t,z)=0$.
However it may be the case that D[B[t, z], z] has a dependence on w[t, z] or q[t, z] with D[w[t, z], t] having also a dependance on B[t, z] in which case the PDE's are coupled and can not be integrated indpendently from one another.
So it is technically important to find out what is wrong with IBVP2.
I would appreciate any help on the above.
PS: My real concern is to tackle problems where the PDE's are coupled and mix temporal and spatial derivatives for example $$\partial_tw=e^B\cdot\partial_zq+w\cdot\partial_zw\qquad\partial_tq=e^B\cdot\partial_zw+w\cdot\partial_zq\qquad\partial_zB=w\cdot e^q$$ so I need an answer that can be generalised in this case.
I am not sure whether Μathematica can tackle problems of this kind in general. However it is hard to believe that it crushes for this -apparently- trivial case.
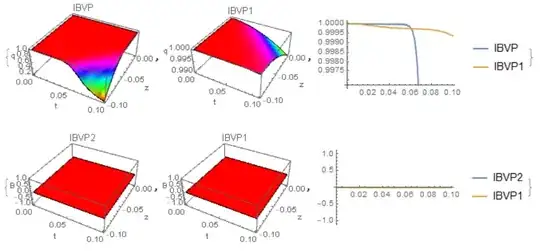

NDSolvecan't handle PDE that doesn't involve pure derivative of time well (at least now) . Similar problems: https://mathematica.stackexchange.com/q/184281/1871 https://mathematica.stackexchange.com/q/163923/1871 https://mathematica.stackexchange.com/q/183745/1871 https://mathematica.stackexchange.com/q/118194/1871 https://mathematica.stackexchange.com/q/133731/1871 – xzczd Jan 09 '19 at 08:53NDSolvecan handle PDE that doesn't involve pure derivative of time. Have you seen this post? – dkstack Jan 09 '19 at 09:10bcart, it's simple, just modify the additional equation toD[D[B[t, z], z] == 0, t]. Then you'll find Mathematica still can't solve the system, and this is where the real trouble begins. Also, notice in Alex's answer linked above,NDSolveactually doesn't analyse the PDE system correctly, either. For more information, check my comment under that answer. – xzczd Jan 09 '19 at 12:32B[0, z] == 0, B[t, 0] == 0along with PDED[B[t, z], z] == 0lead to $B(t,z)=0$. How can an infinite number of functions satisfy these? – dkstack Jan 09 '19 at 13:22