Help in advection-dispersion equation using NDSolveValue

Question

i have the advection-dispersion equation:

Dz = 0.0000738739; as = 2.21622*10^-6;
Dz*D[u[z, t], z, z] - as*D[u[z, t], z] == D[u[z, t], t] 

The boundary and initial conditions are:

u[z, 0] == 0.10, 
u[0, t] == 0.30, , (D[u[z, t], z] /. z -> Infinity) == 0

As i wanted to solve numerically, i changed "infinity" to 10^5 and tried to solve the pde numerically with the following code:

 pde = {Dz*D[u[z, t], z, z] - as*D[u[z, t], z] - D[u[z, t], t] == 0, 
  u[z, 0] == 0.1, 
  u[0, t] == 
   0.30 + (0.10 - 0.30)*Exp[-100000*t], (D[u[z, t], z] /. 
     z -> 10^5) == 0}

solution = NDSolveValue[pde, u, {z, 0, 100000}, {t, 0, 100000}]

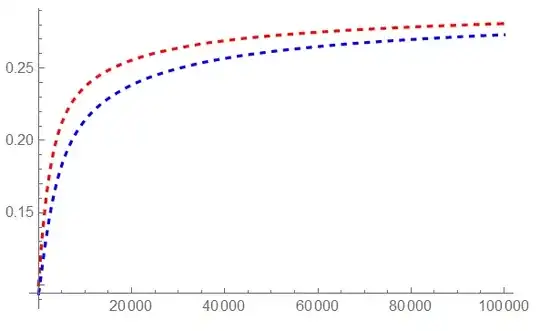
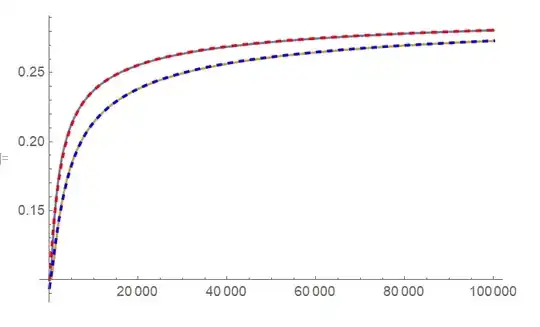
Plot[solution[0.6, t], {t, 0, 100000}, PlotRange -> All]

The Exp[-100000*t] term was used to not give inconsisting boundary condition values. The problem is that when i plot the solution, the results are totally wrong comparing to the reality and also to the analitic solution of this pde. I've tried to use the NeumannValue and DirichletCondition functions, i get better results, close to the analitical solution, but still very different from the analitic solution. And i don't know why the results change when i use the NeumannValue and DirichletCondition functions, in my mind they should be the same, as i wrote the code correctly. Here is the analitic solution of the proposed PDE.

z1[z_, t_, as_, Dz_] := (z + as*t)/(2*Sqrt[Dz*t])

z2[z_, t_, as_, Dz_] := (z - as*t)/(2*Sqrt[Dz*t])

A[z_, t_, as_, Dz_] := 
 1/2 (Erfc[z1[z, t, as, Dz]] + Exp[((as*z)/Dz)]*Erfc[z2[z, t, as, Dz]])

u[z_, t_, u0_, ui_, as_, Dz_] := ui + (u0 - ui)*A[z, t, as, Dz]

Plot[{u[0.6, t, 0.30, 0.10, as, Dz]}, {t, 0.01, 1000000}, PlotRange -> All]

Can anybody, please, help me to find the solution to this problem? Thanks!

Answer 1

First of all, the given analytic solution is incorrect:

Clear[as, Dz]; 
func = {z, t} \[Function] u[z, t, u0, ui, as, Dz]; 
error = Dz*D[u[z, t], z, z] - as*D[u[z, t], z] - D[u[z, t], t] /. u -> func; 
Plot3D[
 Block[{u0 = 1, ui = 3, as = 1, Dz = 1}, error] // Evaluate, {t, 0, 1}, {z, 0, 1}, 
 PlotPoints -> 50]

Then the problem is related to this one. The numeric solution given by NDSolve is inaccurate, because the domain of z isn't properly chosen. Notice the values of as and Dz are very small, this suggest the variation of the solution will only happen in a small area near z == 0, and the default spatial grid (only 25 points in z direction) is not dense enough to capture the variation. So the simplest solution is to chose a smaller number for approximation of $\infty$:

Dz = 0.0000738739; as = 2.21622*10^-6;
tend = 1/100; zend = 1/200;
pde = {Dz D[u[z, t], z, z] - as D[u[z, t], z] - D[u[z, t], t] == 0, u[z, 0] == 0.1, 
   u[0, t] == 0.30 + (0.10 - 0.30) Exp[-100000 t], (D[u[z, t], z] /. z -> zend) == 0};

solution = NDSolveValue[pde, u, {z, 0, zend}, {t, 0, tend}];

Plot3D[solution[z, t], {z, 0, zend}, {t, 0, tend}, PlotRange -> All]

Answer 2

Hello @xzczd thank you for the time you spent in this problem. I have some points to take into consideration.

Fortunately, yesterday i was struggling with this issue and i came up to a solution very similar to yours, because of the discussion we previously had. I realized that the domain was too big and, as the initial conditions are constant, Mathematica thinks that the error is negligible. So i increase the refinement of the grid until it stabilizes. Here is the code:

u0 = 0.30;
ui = 0.10;
ContDireito = 1000;
Dz = 0.00007387387387387386`;
as = 2.2162162162162158`*^-6;

EqNumerica = {Dz*Derivative[2, 0][u][z, t] - 
    as*Derivative[1, 0][u][z, t] - Derivative[0, 1][u][z, t] == 0, 
  u[z, 0] == If[z == 0, u0, ui], 
  u[0, t] == u0, (D[u[z, t], z] /. z -> ContDireito) == 0}

SolutionNew = 
 NDSolveValue[EqNumerica, u, {z, 0, 1}, {t, 0, 10000000}, 
  Method -> {"MethodOfLines", 
    "SpatialDiscretization" -> {"TensorProductGrid", 
      "MinPoints" -> 2000}}]

After that, i plotted SolutionNew:

Of course, this is not the point that deserves an answer. What i would like to discuss is about the analytical solution. First of all, the right-Boundary condition is in infinite, so we need to make sure that the domain is large enough comparing to the points we analyze, that's why i put the domain in 1000. After seeing te convergence (which we could calculate, but it was easier for me to just keep trying until the plotting remains constant) i compared it to the analytic solution, which, according to your code, is obviously wrong. Here is the comparison:

So, what's the point? I couldn't see the proof of this analytic solution, but i suppose it uses some approximations in its deduction, so that for small values of as and Dz it works perfectly. The values of as and Dz that you used were a little bit unrealistic for the studied case. I appreciate If you could do any further collaboration about that. Thanks for the valuable discussion.