VoronoiMesh with custom distance function

Question

I'm failing at reading the documentation. Is there a way to specify the distance function used by VoronoiMesh? As a stripped down example say I have a rank-1 lattice such as:

n = 256; v1 = {1, 71};

points = Table[Mod[i v1, n], {i, 0, n - 1}];
mesh = VoronoiMesh[points, {{0, n - 1}, {0, n - 1}}];
Show[mesh, Graphics[{Orange, Point[points]}]]

but instead of standard Euclidean distance I instead want Euclidean distance on the flat torus, so in this example all the cells would be the same shape.

I don't know of a way to change the distance function in VoronoiMesh, but the "properties and relations" section of the docs shows an example where the conditions for each cell are generated explicitly and the mesh is reproduced with RegionPlot. That's not typically very fast, but it may work for you. What functional expression would "Euclidean distance on the flat torus" have? — MarcoB, Mar 19 '19 at 14:34
Possible duplicate: Voronoi tessellations on meshed surfaces — Szabolcs, Mar 19 '19 at 14:38
Adding a general non-Euclidean metric to the space would, I think, make the problem much harder computationally; it wouldn't necessarily be the case that a "straight line" (geodesic) bisecting the path of minimum distance between two points would be equidistant from both. — Michael Seifert, Mar 19 '19 at 14:40
Also, for your problem, a quick and dirty way to solve the problem would be to "pad" the set of points with duplicate points on all four sides, find the Voronoi mesh of that, and then trim the resulting cells back to the original domain. — Michael Seifert, Mar 19 '19 at 14:42
@ MarcoB: simply the top/bottom edges are the same and likewise right/left (so the square tiles the plane). Assume by brain's working correctly a hacky distance would be: "d[{x0_, y0_}, {x1_, y1_}, n_] := Sqrt[Mod[w[x1 - x0, n], n]^2 + Mod[w[y1 - y0, n], n]^2]" with helper function: w[d_, n_] := With[{a = Abs[d]}, If[a <= n/2, a, n - a]] — MB Reynolds, Mar 19 '19 at 21:17
@ Michael Seifert: padding would certainly work for all the cases I have in mind. — MB Reynolds, Mar 19 '19 at 21:19

score 5 · Answer 1 · answered Mar 20 '19 at 01:00

If you're only concerned about visualization and not computation, you could always create a relation and pass it to a plotting function. If the number of points is low enough and your distance function isn't too unwieldy, you should get ok results.

VoronoiBoundaryPlot[pts_, bds_, df_:EuclideanDistance] :=
  Block[{nf, isoLine, x1, x2, y1, y2, mr, δ = .005, good, keep},
    nf = Nearest[pts -> {"Index", "Element"}, DistanceFunction -> df];
    isoLine[q_] := df[#1, q] - df[#2, q]& @@ Sort[nf[q, {2, ∞}]][[All, 2]];
    {{x1, x2}, {y1, y2}} = bds;

    mr = DiscretizeGraphics[ContourPlot[isoLine[{x, y}] == 0, {x, x1, x2},{y, y1, y2}, PlotPoints -> 80, Evaluated -> False]];
    good = Pick[Range[MeshCellCount[mr, 0]], UnitStep[Abs[isoLine /@ MeshCoordinates[mr]] - δ], 0];
    keep = Cases[Tally[mr["ConnectivityMatrix"[0, 1]][[good]]["NonzeroPositions"][[All, 2]]], {_,2}][[All, 1]];

    Graphics[{
      GraphicsComplex[MeshCoordinates[mr], {Red, MeshCells[mr, {1, keep}]}],
      {Point[pts]}
    }]
  ]

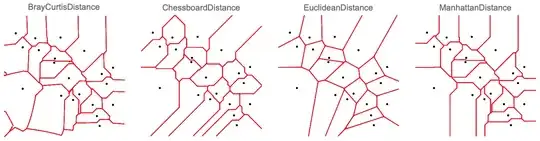
A small example:

SeedRandom[1234];
pts = RandomReal[{0, 1}, {20, 2}];
dfs = {BrayCurtisDistance, ChessboardDistance, EuclideanDistance, ManhattanDistance};
bds = {{-.1, 1.1}, {-.1, 1.1}};

Table[Show[VoronoiBoundaryPlot[pts, bds, df], PlotLabel -> df], {df, dfs}]

VoronoiMesh with custom distance function

1 Answers1