Numerical solution using RK4 to solve nonlinear ODE?

Question

I am trying to use the Runge-Kutta 4 method to solve the nonlinear ODE, using the following Mathematica code:

s = NDSolve[{v'[t] + (v'[t])^3 - (t - 1) == 0, v[0] == 1}, {v}, {t, 0, 1}]

1) I don't know if RK4 is an option for NDSolve[] or not?

2) I need the values of $v$ at $v_k\in\{0.0, 0.1, \dots, 1.0\}$, that is with a step size of $h=0.1$.

Please look here first: [Solving a system of ODEs with the Runge-Kutta method] (https://mathematica.stackexchange.com/questions/23516/solving-a-system-of-odes-with-the-runge-kutta-method/23583#23583) — mjw, Apr 01 '19 at 23:57
Dear mjw, I tried it before but it is provide me complex number in mathematica version 8 and 11, but in v10 it ok, why? I don't know. — user62716, Apr 02 '19 at 09:07
I think because of the non-linearity in your differential equation, there are multiple solutions! Why different versions of Mathematica produce different answers, that I really don't know. — mjw, Apr 02 '19 at 16:47
I personally like to use my own code for RK-4 ( https://mathematica.stackexchange.com/questions/194002/ways-to-speed-up-user-implemented-rk4/194004?noredirect=1#comment505087_194002 ) — Shinaolord, Apr 05 '19 at 22:58
Related: https://mathematica.stackexchange.com/questions/48743/how-can-i-get-the-time-steps-chosen-by-ndsolve-when-the-method-explicitrunge/109879#109879, https://mathematica.stackexchange.com/questions/184132/debugging-ndsolve-to-see-numerical-values-at-each-time-step/184251#184251, https://mathematica.stackexchange.com/questions/56458/how-do-get-an-output-table-or-a-plot-of-individual-variables-from-ndsolve-output — Michael E2, Apr 06 '19 at 01:08
@Shinaolord The reason that (by default) you can't get less than 10 steps is that the default for MaxStepFraction is 1/10. Pass the option MaxStepFraction -> 1 and you should be able to get whatever step size you like — Michael E2, Apr 06 '19 at 12:41

score 6 · Answer 1 · answered Apr 06 '19 at 02:33

The built-in "ExplicitRungeKutta" method of order 4 is an "embedded" method (i.e., with an embedded error estimation method). Here is the classical method (with code cribbed from this answer by J.M.):

ClassicalRungeKuttaCoefficients[4, prec_] := 
  With[{amat = {{1/2}, {0, 1/2}, {0, 0, 1}}, 
    bvec = {1/6, 1/3, 1/3, 1/6}, cvec = {1/2, 1/2, 1}}, 
   N[{amat, bvec, cvec}, prec]];

Here is a comparison with the built-in method:

NDSolve`EmbeddedExplicitRungeKuttaCoefficients[4, MachinePrecision]
ClassicalRungeKuttaCoefficients[4, MachinePrecision]
(*
{{{0.4`},
  {-0.15`, 0.75`},
  {0.4318181818181818`, -0.3409090909090909`, 0.9090909090909091`},
  {0.1527777777777778`, 0.3472222222222222`, 0.3472222222222222`, 0.1527777777777778`}},
 {0.1527777777777778`, 0.3472222222222222`, 0.3472222222222222`, 0.1527777777777778`, 0.`},
 {0.4`, 0.6`, 1.`, 1.`},
 {0.013269665336144196`, -0.06634832668072098`, 0.06634832668072098`,
  0.14596631869758617`, -0.15923598403373035`}}

{{{0.5`},
  {0.`, 0.5`},
  {0.`, 0.`, 1.`}},
 {0.16666666666666666`, 0.3333333333333333`, 0.3333333333333333`, 0.16666666666666666`},
 {0.5`, 0.5`, 1.`}}
*)

Here's a way to get the solution steps, based on some of the links I put in a comment above:

vf = v /. 
   First@NDSolve[{v'[t] + (v'[t])^3 - (t - 1) == 0, v[0] == 1}, {v}, {t, 0, 1}, 
     Method -> {"FixedStep", 
       Method -> {"ExplicitRungeKutta", "DifferenceOrder" -> 4, 
         "Coefficients" -> ClassicalRungeKuttaCoefficients}}, 
     StartingStepSize -> 1/10];

Transpose@Flatten[vf[{"Coordinates", {"ValuesOnGrid"}}], 1]
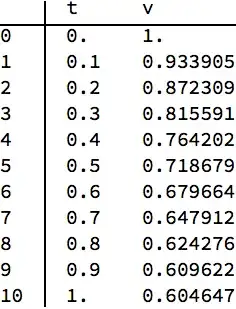
TableForm[%, TableHeadings -> {Range[0, 10], {t, v}}]
(*
  {{0., 1.}, {0.1, 0.933905}, {0.2, 0.872309}, {0.3, 0.815591}, {0.4, 0.764202},
   {0.5, 0.718679}, {0.6, 0.679664}, {0.7, 0.647912}, {0.8, 0.624276},
   {0.9, 0.609622}, {1., 0.604647}}
*)

Mathematica graphics

Numerical solution using RK4 to solve nonlinear ODE?

1 Answers1

Linked