Plot of Laguerre-Gaussian wavefront

Question

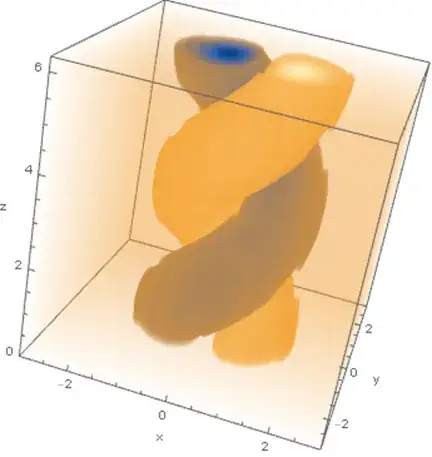
I have tried to plot the wavefront of a Laguerre-Gaussian beam, I know that to do that I have to plot the set of all points where the wave has the same phase.

I have try to use the conditional If to do it but the program just don't do it

LG[r_, ϕ_, p_, l_, 
  w_] := (Sqrt[(2 p!)/(π (p + Abs[l])!)] 1/
    w E^(-r^2/w^2) ((r Sqrt[2])/w)^Abs[l] LaguerreL[p, Abs[l], 
    2 r^2/w^2] E^(I l ϕ))
Module[{l = 1, p = 0, xMax = 3, zMax}, zMax = 2 Pi ;
 DensityPlot3D[If[Cos[I( l ϕ -I z)==0,
  Re[LG[Sqrt[x^2 + y^2], ArcTan[x, y], p, l, 1] Exp[-I z]]], {x, -xMax,
    xMax}, {y, -xMax, xMax}, {z, 0, zMax}, PlotPoints -> 60, 
  AxesLabel -> {"x", "y", "z"}]]

I would like to obtain something like

Ref: https://en.wikipedia.org/wiki/Orbital_angular_momentum_of_light

Show and write the complete your code in order to obtain any suggestion or comments, it helps also this community to solve similar problems. — irondonio, Jul 26 '19 at 09:34
Your code sample involves typo, please double check it. Then, related: https://mathematica.stackexchange.com/q/177210/1871 — xzczd, Jun 09 '21 at 11:33
did you able to plot the wavefront of laguerre gaussian? if so please help me to plot — Jigme, Jun 09 '21 at 09:11

score 3 · Answer 1 · edited Jun 09 '21 at 15:39

Without arrow in the first line it can be preproduced with this code

LG[r_, ϕ_, p_, l_, w_, 
   z_] := (Sqrt[(2 p!)/(π (p + Abs[l])!)] 1/
     w E^(-r^2/w^2) ((r Sqrt[2])/w)^Abs[l] LaguerreL[p, Abs[l], 
     2 r^2/w^2] E^(I l ϕ + I z));
LGA[r_, p_, l_, w_, z_] := 
  Sqrt[(2 p!)/(π (p + Abs[l])!)] 1/w E^(-r^2/w^2) ((r Sqrt[2])/w)^
    Abs[l] LaguerreL[p, Abs[l], 2 r^2/w^2];
{Table[Module[{l = L, p = 0, w = 1}, 
   ParametricPlot3D[{Cos[u] Sin[v], Sin[u] Sin[v], l u}, {u, 0, 
      2 Pi}, {v, -Pi, Pi}, Mesh -> None, 
     ColorFunction -> 
      Function[{x, y, z}, 
       Hue[Abs[LG[Sqrt[x^2 + y^2], ArcTan[x, y], p, l, w, z]]]], 
     Boxed -> False, BoxRatios -> {1, 1, 1}, Axes -> False, 
     PlotPoints -> 50, PlotLabel -> Row[{"l = ", l}], 
     ColorFunctionScaling -> False] // Quiet], {L, -2, 2}], 
 Table[Module[{l = L, p = 0, w = 1}, 
   DensityPlot[
     Arg[ LG[Sqrt[x^2 + y^2], ArcTan[x, y], p, l, w, 0]], {x, -3, 
      3}, {y, -3, 3}, Frame -> False, Axes -> False, PlotPoints -> 50,
      ColorFunction -> Hue] // Quiet], {L, -2, 2}], 
 Table[Module[{l = L, p = 0, w = 1}, 
   DensityPlot[
     Abs[LGA[Sqrt[x^2 + y^2], p, l, w, 0]], {x, -3, 3}, {y, -3, 3}, 
     Frame -> False, Axes -> False, PlotPoints -> 50, 
     ColorFunction -> Hue, PlotRange -> All] // Quiet], {L, -2, 2}]}

Plot of Laguerre-Gaussian wavefront

1 Answers1

Linked