I am trying to plot wavefronts of Laguerre-Gaussian modes, and want to show the changing number of twists with the change in l values. If anyone has the code or any insights. Kindly help me about it. I want something like this.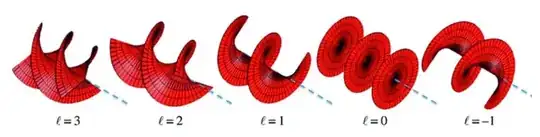
1 Answers
Code to reproduce $l$ periods on $(0, 2\pi)$ can be modified from our answer here as follows
LG[r_, \[Phi]_, p_, l_, w_,
z_] := (Sqrt[(2 p!)/(\[Pi] (p + Abs[l])!)] 1/
w E^(-r^2/w^2) ((r Sqrt[2])/w)^Abs[l] LaguerreL[p, Abs[l],
2 r^2/w^2] E^(I l \[Phi] + I z));
LGA[r_, p_, l_, w_, z_] :=
Sqrt[(2 p!)/(\[Pi] (p + Abs[l])!)] 1/w E^(-r^2/w^2) ((r Sqrt[2])/w)^
Abs[l] LaguerreL[p, Abs[l], 2 r^2/w^2];
{Table[Module[{l = L, p = 0, w = 1},
ParametricPlot3D[{Cos[l u] Sin[v], Sin[Abs[l] u] Sin[v], l u}, {u,
0, 2 Pi}, {v, -Pi, Pi}, Mesh -> None,
ColorFunction ->
Function[{x, y, z},
Hue[Abs[LG[Sqrt[x^2 + y^2], ArcTan[x, y], p, l, w, z]]]],
Boxed -> False, BoxRatios -> {1, 1, 1}, Axes -> False,
PlotPoints -> 50, PlotLabel -> Row[{"l = ", l}],
ColorFunctionScaling -> False, PlotRange -> All] //
Quiet], {L, {-2, -1, 1, 2, 3}}],
Table[Module[{l = L, p = 0, w = 1},
DensityPlot[
Arg[LG[Sqrt[x^2 + y^2], ArcTan[x, y], p, l, w, 0]], {x, -3,
3}, {y, -3, 3}, Frame -> False, Axes -> False, PlotPoints -> 50,
ColorFunction -> Hue] // Quiet], {L, {-2, -1, 1, 2, 3}}],
Table[Module[{l = L, p = 0, w = 1},
DensityPlot[
Abs[LGA[Sqrt[x^2 + y^2], p, l, w, 0]], {x, -3, 3}, {y, -3, 3},
Frame -> False, Axes -> False, PlotPoints -> 50,
ColorFunction -> Hue, PlotRange -> All] // Quiet], {L, {-2, -1,
1, 2, 3}}]}
- 44,369
- 3
- 48
- 106

Tour. Subsequently, post an on-topic question along with a minimal example and properly formatted Mathematica code that you have tried so far. Thanks. – Syed Sep 06 '23 at 06:39lperiods? – Alex Trounev Sep 06 '23 at 11:59