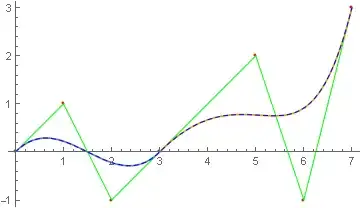
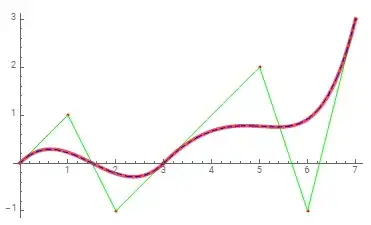
I would like to use BezierCurve with npts=7 and SplineDegree -> 3 and access its BezierFunction. This code helps:
pts = {{0, 0}, {1, 1}, {2, -1}, {3, 0}, {5, 2}, {6, -1}, {7, 3}};
f1 = BezierFunction[pts[[1;;4]]]
f2 = BezierFunction[pts[[4;;7]]]
Show[Graphics[{Red, Point[pts], Green, Line[pts]}, Axes -> True],
ParametricPlot[{f1[t],f2[t]}, {t, 0, 1}],Graphics[{Blue, Dashed,
BezierCurve[pts, SplineDegree -> 3]}]]
Can it be done better, defining f as a single function, whose plot is BezierCurve?