I wish to find the smallest distance from a point to a curved defined via a Bézier function. I want to do this automatically. For particular cases it is not to difficult. Here is a minimum working example. What point on the curve is closest to the red point?
pts = {{-3, 0}, {-1, 3}, {1, -3}, {0, 1}, {0, 2}, {2, 2}, {-2, -2}};
pt = {-0.07194, 0.6342};
Graphics[{BezierCurve[pts], Point[pts], Red, Point[pt]},
Frame -> True]
My first attempt was RegionDistance[] but this does not have BezierCurve as an input. Looking about I found BezierFunction which enables me to make a function that gets the distance to the curve as a parameter of distance along the curve. Thus
ClearAll[f, f1];
f = BezierFunction[pts];
f1[t_?NumberQ] := EuclideanDistance[ f[t], pt]
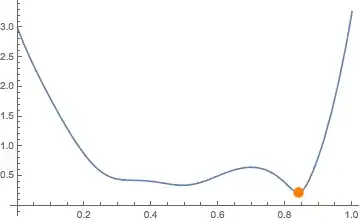
Plot[f1[t], {t, 0, 1}]
I was now able to look for the minimum using FindMinimum. This produced an error without a starting point. However, the point I got was not the minimum.
{min, pos} = FindMinimum[f1[t], {t, 0.5}];
minpt = f1[t /. pos];
Plot[f1[t], {t, 0, 1},
Epilog -> {Orange, PointSize[0.03], Point[{minpt, f1[minpt]}]}]
I am aware that finding global minima is not easy so before I try and resolve that issue I wish to return to the original problem and see if anyone can come up with a good method. Thanks
***** Edit*****
Thanks to all who answered. You have taught me much about splines. Clearly BezierFunction is not as good as BSplineFunction. So I perhaps should use BSplineCurve rather than BezierCurve. Are there discussions on which is most suitable when? @flinty has made some very good points in his reply.
Due to the difficulty of local minima it seems that using FindMinimum is not a suitable approach. The best approaches seems to be that of kglr and Chip Hurst. I have opted for the solution of kglr for now (mainly because I started working on that one first). Here is the module I put together to find the point.
nearestPointOnCurve[pts_List, None, sfy_] := {};
nearestPointOnCurve[pts_List, pt_List, sfy_] :=
Module[{distFun, g, lines, points, p1, p2},
distFun[{x1_, y1_}, {x2_, y2_}] :=
Sqrt[((x2 - x1))^2 + (sfy (y2 - y1))^2];
g = Graphics[{BezierCurve[pts]}, PlotRange -> All, AspectRatio -> 1];
lines = MeshPrimitives[DiscretizeGraphics[g], 1];
points = Flatten[Cases[lines, Line[a_] :> a, \[Infinity]], 1];
p1 = First@Nearest[points, pt, DistanceFunction -> distFun];
p1]
You can see I have put in a distance function because sometimes you need the location of the point nearest the cursor rather than the nearest Cartesian point. Here is an example that illustrates this point and is something to play with.
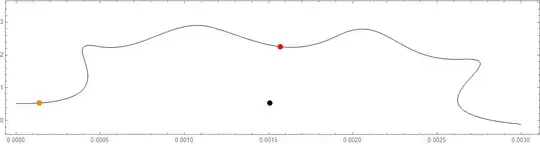
pts = {{0, 0.5178`4.}, {0.0007762`4., 0.4642`4.}, {0.0001964`4.,
2.535`4.}, {0.000477`4., 2.268`4.}, {0.0007575`4.,
2.`4.}, {0.0009247`4., 3.202`4.}, {0.001171`4.,
2.834`4.}, {0.001418`4., 2.466`4.}, {0.001614`4.,
1.833`4.}, {0.001908`4., 2.586`4.}, {0.002202`4.,
3.338`4.}, {0.002247`4., 1.774`4.}, {0.002647`4.,
1.87`4.}, {0.003048`4., 1.966`4.}, {0.002157`4.,
0.2631`4.}, {0.003`4., -0.1185`4.}};
{x1, x2} = MinMax[pts[[All, 1]]];
{y1, y2} = MinMax[pts[[All, 2]]];
ar = 1/4;
{sfx, sfy} = {1/(x2 - x1), ar/(y2 - y1)};
DynamicModule[{},
Dynamic[Graphics[{BezierCurve[pts], PointSize[0.01],
Point[MousePosition["Graphics"]],
Red, Point[
nearestPointOnCurve[pts, MousePosition["Graphics"], sfy/sfx]],
Orange,
Point[nearestPointOnCurve[pts, MousePosition["Graphics"], 1]]
}, Frame -> True, PlotRange -> All, AspectRatio -> ar,
ImageSize -> 12 72]
]
]
The black point is the cursor, the orange point is the nearest in Cartesian distance and the red point is the nearest in the screen coordinates.
Thanks for all your help.




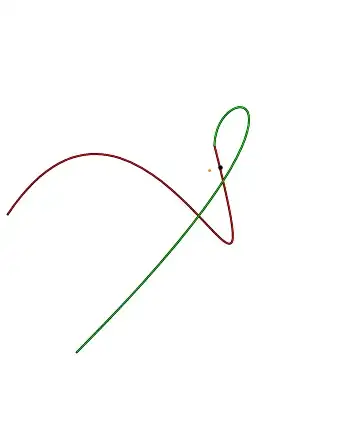


bf = BezierFunction[pts]; minB[t_?NumericQ] := SquaredEuclideanDistance[bf[t], pt]; tm = NArgMin[{minB[t], 0 < t < 1}, t]; Graphics[{BezierCurve[pts], Point[pts], Red, Point[pt], Point[bf[tm]]}, Frame -> True];There are better ways to do it, but I don't have time to write it up for now. – J. M.'s missing motivation May 21 '20 at 13:24Graphics[{Line[Table[bf[t], {t, 0, 1, .01}]], Point[pts], Red, Point[pt], Point[bf[tm]]}, Frame -> True]you get a different curve. Your nearest point is not the nearest to the desired point on theBezierCurve– flinty May 21 '20 at 13:31b = BezierFunction[pts]; Graphics[{Red, BezierCurve[pts], Green, Line[Table[b[t], {t, 0, 1, .01}]]}]– flinty May 21 '20 at 13:57BezierFunction[]withBSplineFunction[], please? – J. M.'s missing motivation May 21 '20 at 14:00BSpineFunction[]has a closer shape but it's still off and the loop is bigger. Have we uncovered a bug? - edit: see here: https://mathematica.stackexchange.com/questions/186949/beziercurve-is-different-from-bezierfunction Apparently you need to use SplineDegree -> (Length@pts - 1) – flinty May 21 '20 at 14:02FindMinimumon your graph off[t], it should bePoint[{t /. pos, minpt}], notPoint[{minpt, f1[minpt]}]. Running the code with this fix shows thatFindMinimumfound the shallow local minimum at $ t \approx 0.5$. – Michael Seifert May 21 '20 at 14:41