3

I have following expression

$$-3 b_{\sigma _d}-3 b_{\sigma _v}-b-b_2+2 j-2 j_2-2 j_3+2 j_6+12$$

Mathematica input

12-b+2 j-Subscript[b, 2]-3 Subscript[b, Subscript[\[Sigma], d]]-3 Subscript[b, Subscript[\[Sigma], v]]-2 Subscript[j, 2]-2 Subscript[j, 3]+2 Subscript[j, 6]

I want to reorder this expression by partitioning the occuring symbols. Additionally, common factors of the partitions should be factored out:

Partition (given by user): $$\{\{j,j_2,j_3,j_6\},\{b,b_2,b_{\sigma_d},b_{\sigma _v}\}\}$$

The order should also be respected. The end result would look like $$2(j-j_2-j_3+j_6)-(b+b_2+3 b_{\sigma _d}+3 b_{\sigma _v})+12$$

I have considered FactorTerms[poly,{x_1,x_2,...] and Collect[expr,{x_1,x_2,...}] but was not successful to achieve this.

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
Hotschke
  • 707
  • 3
  • 11

2 Answers2

5
expr = 12 - b + 2 j - Subscript[b, 2] - 
 3 Subscript[b, Subscript[σ, d]] - 
 3 Subscript[b, Subscript[σ, v]] - 2 Subscript[j, 2] - 
 2 Subscript[j, 3] + 2 Subscript[j, 6]

Inactive[Plus] @@ 
  (Total /@ Join @@ 
     GatherBy[List @@ expr, MatchQ[_ (# | Subscript[#, _])] & /@ {j, b}])

TeXForm @ %

$\Large 12+\left(-3 b_{\sigma _d}-3 b_{\sigma _v}-b-b_2\right)+\left(2 j-2 j_2-2 j_3+2 j_6\right)$

Update:

ClearAll[f]
f[e_] := Row @ Flatten @ Append[Reverse @ Values @ 
   GroupBy[Transpose[{Coefficient[e, #], #}& @ Variables[e]] /.
      {a_, b_Symbol} :> {a, Subscript[b, 0]}, #[[2,1]]&, 
     Row[{# /. { 1 -> " + ", -1 -> " - "}, "(", HoldForm @ #2, ")"}]& @@ 
     FactorList[ Dot @@ Transpose[#]][[All, 1]]&],
      If[# < 0, {" - ", -#}, {" + ", #}]&[e /.
       (Alternatives@@Variables[e] -> 0)] /. {_, 0} -> Nothing] /.
    Subscript[a_, 0] -> a

Examples:

f @ expr

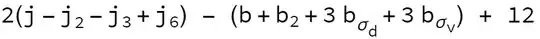
enter image description here

System`Convert`CommonDump`templateBoxToDisplay = BoxForm`TemplateBoxToDisplayBoxes;

TeXForm @ f @ expr

$\Large 2(j-j_2-j_3+j_6)\text{ - }(b+b_2+3 b_{\sigma _d}+3 b_{\sigma _v})\text{ + }12$

f[- expr - 20] // TeXForm

$\Large -2(j-j_2-j_3+j_6)\text{ + }(b+b_2+3 b_{\sigma _d}+3 b_{\sigma _v})\text{ - }32$

Note: I used Carl's answer from this q/a to make TeXForm process Rows properly.

kglr
  • 394,356
  • 18
  • 477
  • 896
  • 1
    Thank you very much for your answer and update. Unfortunately, I can only upvote once as always. Sometimes I feel like I would like to upvote several times for an answer based on knowlege which I could not gain on my own in a reasonable amount of time. – Hotschke Aug 11 '19 at 12:55
  • A small improvement to f[e_] would be to not print + 0 if there is not a constant number. If you know this quickly, I again would appreciate your help. I am still dissecting your f. – Hotschke Aug 13 '19 at 13:41
  • 1
    @Hotschke, the updated version should remove +/- 0. – kglr Aug 13 '19 at 13:55
  • I was planning to use Switch[] but /. {_, 0} -> Nothing looks now like a quite easy fix. – Hotschke Aug 13 '19 at 14:18
0

A minor variant of the answer by kglr:

  • explicit partition $$\texttt{GatherBy}\left[\texttt{List}\text{@@}\text{expr},\left\{\texttt{MatchQ}\left[\_ \left(b\left|b_2\right|b_{\sigma _d}|b_{\sigma _v}\right)\right],\texttt{MatchQ}\left[\_ \left(j\left|j_2\right|j_3|j_6\right)\right]\right\}\right]$$
  • Added Factor[] which moves the common factor 2 of the j's in front of the parenthesis
  • Added Reverse[] to get desired order (+12 at the end)
  • Use Cases[lis, {Except[_List] ..}, -2] to remove intermediate lists created by GatherBy[list,{f_1,f_2,...}] (from How can I Flatten this List with Inner List of Lists?)
  • Prepending StandardForm for TeXForm seems to keep the order.
expr = 12 - b + 2 j - Subscript[b, 2] - 
 3 Subscript[b, Subscript[σ, d]] - 
 3 Subscript[b, Subscript[σ, v]] - 2 Subscript[j, 2] - 
 2 Subscript[j, 3] + 2 Subscript[j, 6]

p = {MatchQ[_ (j | Subscript[j, 2] | Subscript[j, 3] | Subscript[j, 
   6])], MatchQ[_ (b | Subscript[b, 2] | Subscript[b, 
   Subscript[\[Sigma], d]] | Subscript[b, Subscript[\[Sigma], 
   v]])]};

list = Reverse[Cases[GatherBy[List @@ expr, p], {Except[_List] ..}, -2]]

Inactive[Plus] @@ Factor /@ Total /@ list

TeXForm @ StandardForm @ %

$$2 \left(j-j_2-j_3+j_6\right)+\left(-b-b_2-3 b_{\sigma _d}-3 b_{\sigma _v}\right)+12$$

Remaining improvements would be

  • placing common minus sign of the b's in front of the parenthesis (in general the first symbol in partition should determine the factored sign).
    Why does Factor[-2 a - 2 b] gives -2 (a + b) but Factor[- a - b] again - a - b?
Hotschke
  • 707
  • 3
  • 11