Polar contour plot in Mathematica?

Question

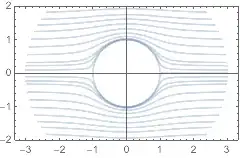
I am following a text on fluid mechanics with MAPLE examples. I want to do the following ContourPlot in Mathematica in Polar coordinates:

$$ (r^2-\frac{a^3}{r}) \sin^{2}\theta$$

where $a=1$

cValues = {0.00001, 0.01, 0.05, 0.1, 0.3, 0.6, 1.0, 1.5, 2.0, 2.5, 3.2}

This is a ContourPlot in Polar coordinates.

$$ (r^2-\frac{a^3}{r}) \sin^{2}\theta=C $$

$C$ is a constant. Notice that MAPLE requires the user to specify the values of $C$.

What is a simple, convenient way to implement polar contour plots?

Note. The picture above represents a sphere at rest in an infinite stream of an ideal fluid. The system is axially symmetric, hence we can use Polar coordinates (instead of Spherical coordinates).

cValues = {0.00001, 0.01, 0.05, 0.1, 0.3, 0.6, 1.0, 1.5, 2.0, 2.5, 3.2} — Conor, Aug 17 '19 at 14:19
they are arbitrary, I just want to make something that looks like the picture above — Conor, Aug 17 '19 at 14:19
Strongly related, if not duplicate: https://mathematica.stackexchange.com/q/67261/1871 — xzczd, Aug 17 '19 at 14:37
A new approach https://mathematica.stackexchange.com/a/300018/72111 — cvgmt, Mar 05 '24 at 22:51

kglr · Accepted Answer · 2019-08-17T17:37:27.250

You can use TransformedField to get a function that can be used as the first argument of ContourPlot:

 f = (r^2 - a^3/r) Sin[t]^2;
 tf = TransformedField[ "Polar" -> "Cartesian", f, {r, t} -> {x, y}]

TeXForm @ tf

$\frac{y^2 \left(x^2 \sqrt{x^2+y^2}+y^2 \sqrt{x^2+y^2}-1\right)}{\left(x^2+y^2\right)^{3/2}}$

cValues = {0.00001, 0.01, 0.05, 0.1, 0.3, 0.6, 1.0, 1.5, 2.0, 2.5, 3.2};
a = 1;

ContourPlot[tf, {x, -3, 3}, {y, -3, 3}, 
  Contours -> cValues, 
  PlotPoints-> 200,
  Axes -> True,
  Frame -> False,
  PlotRange -> All, 
  ContourShading -> None, 
  AspectRatio -> Automatic,
  RegionFunction -> (Norm[{#, #2}] <= 3&)]

An alternative approach is to use f with ContourPlot and post-process the output to transform the lines:

cp1 = ContourPlot[f, {r, 0, 3}, {t, -Pi, Pi}, 
       Contours -> cValues, PlotRange -> All, 
       ContourShading -> None,  Axes -> True, 
       Frame -> False, ImageSize -> 300];

cp2 = Show[cp1 /. GraphicsComplex[c_, rest___] :> 
        GraphicsComplex[c /. {a_, b_} :> (a {Cos[b], Sin[b]}), rest], 
    AspectRatio -> Automatic, ImageSize -> 300];

Row[{cp, cp2}, Spacer[15]]

See also https://mathematica.stackexchange.com/a/67275/4999 for @Kuba's use of TransformedField in this way. — Michael E2, Aug 17 '19 at 21:52

score 10 · Answer 2 · answered Aug 17 '19 at 15:47

Using MeshFunctions and Mesh in a ParametricPlot of polar coordinates to define the contours:

cValues = {0.00001, 0.01, 0.05, 0.1, 0.3, 0.6, 1.0, 1.5, 2.0, 2.5, 3.2};
Block[{a = 1},
 ParametricPlot[r {Cos[\[Theta]], Sin[\[Theta]]},
  {r, 0, 3 a}, {\[Theta], 0, 2 Pi},
  PlotStyle -> None, BoundaryStyle -> None, PlotPoints -> {60, 120},
  MeshFunctions ->
   {Function[{x, y, r, \[Theta]}, (r^2 - a^3/r) Sin[\[Theta]]^2]}, 
  Mesh -> {cValues}, 
  MeshStyle -> {Directive[ColorData[97][1], AbsoluteThickness[1.6]]}, 
  PlotRange -> {All, {-2, 2}}, Method -> {"BoundaryOffset" -> True}]
 ]

score 8 · Answer 3 · answered Aug 17 '19 at 14:45

As mentioned above, I think this problem may be considered as a duplicate, but let me show the usage of my implicitPlot anyway:

cValues = {0.00001, 0.01, 0.05, 0.1, 0.3, 0.6, 1.0, 1.5, 2.0, 2.5, 3.2};

With[{a = 1}, 
 implicitPlot[(r^2 - a^3/r) Sin[theta]^2, {r, 0, 3}, {theta, 0, 2 Pi}, "Polar", 
  PlotPoints -> 25, Contours -> cValues]]

You can of course create the graphic in a way more similar to Maple:

With[{a = 1}, 
 implicitPlot[(r^2 - a^3/r) Sin[theta]^2 == #1, {r, 0, 3}, {theta, 0, 2 π}, "Polar", 
     PlotPoints -> 51, AspectRatio -> Automatic] & /@ cValues // Show]

score 8 · Answer 4 · answered Aug 17 '19 at 14:51

Here is how to do the coordinate system conversion by hand:

cValues = {0.00001, 0.01, 0.05, 0.1, 0.3, 0.6, 1.0, 1.5, 2.0, 2.5, 
   3.2};

ContourPlot[
 (Norm[{x, y}]^2 - 3/Norm[{x, y}]) Sin[ArcTan[x, y]]^2,
 {x, -3, 3},
 {y, -3, 3},
 Contours -> cValues
 ]

Mathematica graphics

OkkesDulgerci · Answer 5 · 2019-08-17T19:36:15.387

Here is an alternative way. We can solve for r and plot $[\theta,r]$.

Solve[(r^2 - a^3/r) Sin[θ]^2 == g, r]

$\left\{\left\{r\to \frac{\sqrt[3]{2} g}{\sqrt[3]{\sqrt{729 \sin ^{12}(\theta )-108 g^3 \sin ^6(\theta )}+27 \sin ^6(\theta )}}+\frac{\csc ^2(\theta ) \sqrt[3]{\sqrt{729 \sin ^{12}(\theta )-108 g^3 \sin ^6(\theta )}+27 \sin ^6(\theta )}}{3 \sqrt[3]{2}}\right\},\\ \left\{r\to -\frac{\left(1+i \sqrt{3}\right) g}{2^{2/3} \sqrt[3]{\sqrt{729 \sin ^{12}(\theta )-108 g^3 \sin ^6(\theta )}+27 \sin ^6(\theta )}}-\frac{\left(1-i \sqrt{3}\right) \csc ^2(\theta ) \sqrt[3]{\sqrt{729 \sin ^{12}(\theta )-108 g^3 \sin ^6(\theta )}+27 \sin ^6(\theta )}}{6 \sqrt[3]{2}}\right\},\\ \left\{r\to -\frac{\left(1-i \sqrt{3}\right) g}{2^{2/3} \sqrt[3]{\sqrt{729 \sin ^{12}(\theta )-108 g^3 \sin ^6(\theta )}+27 \sin ^6(\theta )}}-\frac{\left(1+i \sqrt{3}\right) \csc ^2(\theta ) \sqrt[3]{\sqrt{729 \sin ^{12}(\theta )-108 g^3 \sin ^6(\theta )}+27 \sin ^6(\theta )}}{6 \sqrt[3]{2}}\right\}\right\}$

Let's take real solution.

r[g_, θ_] := (
  2^(1/3) g)/(27 Sin[θ]^6 + 
    Sqrt[-108 g^3 Sin[θ]^6 + 729 Sin[θ]^12])^(1/3) + (
  Csc[θ]^2 (27 Sin[θ]^6 + 
     Sqrt[-108 g^3 Sin[θ]^6 + 729 Sin[θ]^12])^(1/3))/(
  3 2^(1/3))

ListPolarPlot[
 Table[{θ, r[#, θ]}, {θ, 0.01, 2 π, 0.05}] & /@
    cValues // Chop, AspectRatio -> Automatic, 
 PlotRange -> {{-3, 3}, {-2, 2}}, Joined -> True]

Or use PolarPlot

PolarPlot[r[#, θ], {θ, 0.01, 2 π}, 
    AspectRatio -> Automatic, PlotRange -> {{-3, 3}, {-2, 2}}, 
    PlotPoints -> 1000] & /@ cValues // Show

Polar contour plot in Mathematica?

What is a simple, convenient way to implement polar contour plots?

5 Answers5

Linked