3

I deal with two functions f[r,a], where r and a represent modulus and phase of complex number, i.e. z=r*Exp[I*a]. I obtain 2D array in the following way,

lst=Table[Abs[f[r,a]], {a,0,2*Pi,2*Pi/100}, {r,0,1,0.01}]

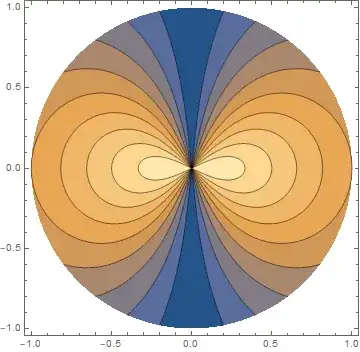
I would like to see for which values of a and r the value of Abs[f[r,a]] is close to 1. To do it, I use ListContourPlot function and obtain

enter image description here

But I have a vague feeling that in my set up it is more appropriate to visualize in polar coordinates. To do it, I perform

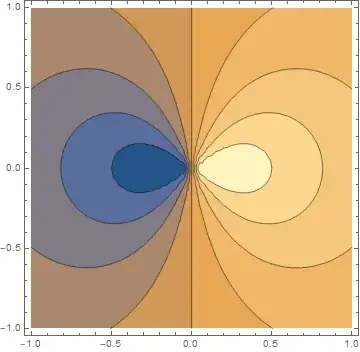
values = Table[{r*Cos[a], r*Sin[a], Abs[f[r,a]},
 {a, 0, 2*Pi, 2*Pi/100}, {r, 0, 1.0, 0.01}]

and then ListContourPlot for obtained values array.

However, resulting plot seems wrong,

fig2

To be honest, I do not understand what did I wrong. I try to find something about ListContourPlot in polar coordinates but it was unsuccessful (for instance, see this).

Let me clarify my point of concern. For simplicity, consider the function

f[r_, a_] := Cos[a]/(1 + r^2).

Having cells evaluated, I obtain

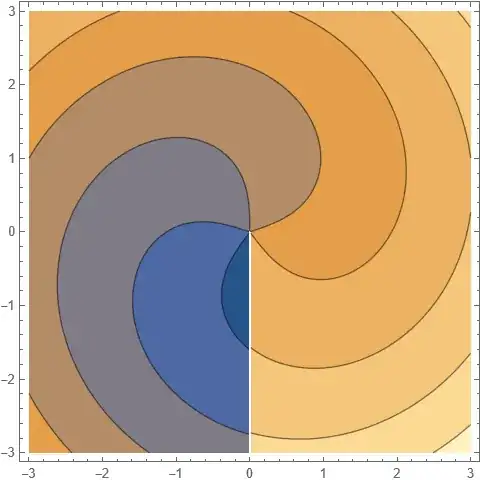
enter image description here

Now, it seems correct to use TransformField

tf = TransformedField["Polar" -> "Cartesian", 
  f[r, a], {r, a} -> {x, y}]

and then use ContourListPlot, which results

enter image description here

The last two pictures are plotted for the same function f but they are different

Artem Alexandrov
  • 803
  • 4
  • 11
  • Your values = Table[Table[{r*Cos[a], r*Sin[a], Abs[f[r, a]}, {a, 0, 2*Pi, 2*Pi/100}, {r, 0, 1.0, 0.01}] is syntactically incorrect. The brackets are pink in the notebook so you should be able to tell they are unmatched. Also Table[Table is unnecessary, as a single Table can already take multiple iterators at the end. The reason it's looking bad is because you need to interpolate those points into a grid for ListContourPlot. Also Abs[f[r,a] is missing a bracket and you need to give a definition of f or at least a simple example one. – flinty Jan 07 '22 at 12:41
  • 1
    This seems to work fine, using my own example f, so most of your issues are syntax related: f[r_, a_] := Cos[a]/(1 + r^2); values = Flatten[Table[ {r*Cos[a], r*Sin[a], Abs[f[r, a]]} , {a, 0, 2*Pi, 2*Pi/100}, {r, 0, 1.0, 0.01} ], 1]; ListContourPlot[values] – flinty Jan 07 '22 at 12:45
  • @flinty the mentioned syntax error comes from copy-paste. I have fixed this issue. The point about interpolation is not clear for me. The very first plot was obtained without any interpolation. My point of concern is that the second plot do not correspond to polar coordinates – Artem Alexandrov Jan 07 '22 at 12:45
  • Yeah actually if you look at ListContourPlot's second form in the docs, you don't need to interpolate into a grid like the first form. All your need is a rank 2 list of {{x,y,z},{x,y,z},...}. Your problem was that you weren't using Flatten[..., 1] like in my example above to remove the extra lists. – flinty Jan 07 '22 at 12:47
  • @flinty I have implicitly assumed Flattent at the first level of list. If not, I would not obtain the 2nd plot from my question – Artem Alexandrov Jan 07 '22 at 12:49
  • Table[{r*Cos[a], r*Sin[a], Abs[f[r, a]]}, {a, 0, 2*Pi, 2*Pi/100}, {r, 0, 1.0, 0.01}], 1]; ListContourPlot[values]``` This should work - but I cannot tell because you haven't provided your `f` – flinty Jan 07 '22 at 12:51

1 Answers1

5

Actually, plotting functions like ContourPlot work just with Cartesian coordinates but one can use the direct form of conversion (R=Sqrt[x^2+y^2], fi=ArcTan[y,x]).

Let's say, we have a function like f=R^2+4 fi:

f = #1^2 + 4 #2 &;

ContourPlot[f[Sqrt[x^2 + y^2], ArcTan[y, x]], {x, -3, 3}, {y, -3, 3}, 
PlotPoints -> 151]

enter image description here

This way you can draw good even the function with an evident singularity.

Rom38
  • 5,129
  • 13
  • 28