Wrapper for inexact numeric complex numbers that maintains polar form

Question

Related question: How can I convert a complex number into an exponent form

Mathematica insists on displaying complex number in form a+I b when a or b are not exact:

Clear["Global`*"]
z = 3 + 4 I;
Abs[z] Exp[I Arg[z]]

z = 3.0 + 4 I;
Abs[z] Exp[I Arg[z]]

What I'd like is a polarForm wrapper that keeps the polar form even when a or b are not exact, like this:

Clear["Global`*"]
(z = 3.0 + 4 I) // polarForm

(z = 3 + 4 I) // polarForm

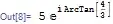
In the above, polarForm is the wrapper needed.

Answer 1

Specify the display format of something using MakeBoxes, like so:

MakeBoxes[polarForm[z_Complex], form_] := 
 With[{r = Abs[z], ϕ = Arg[z]}, 
  RowBox[{If[r == 1, Sequence @@ {}, MakeBoxes[r, form]], 
    If[ϕ == 0, Sequence @@ {}, 
     SuperscriptBox[MakeBoxes[E, form], 
      RowBox[{MakeBoxes["\[ImaginaryI]", form], 
        If[ϕ == 1, Sequence @@ {}, 
         MakeBoxes[ϕ, form]]}]]]}]]

Sqrt[5] E^(I ArcTan[2]) // N // polarForm
(* 2.23607E^(I1.10715) *)

Answer 2

Here's an alternative:

polarForm[z_] := Module[{rt, f},
          If[Im[z] == 0 && Positive[Re[z]], Return[z]];
          rt = Through[{Abs, Arg}[z]];
          f = Which[
                    rt[[1]] == 1, Defer[E^(I #2)] &,
                    rt[[2]] == 1, Defer[#1 E^I] &,
                    True, Defer[#1 E^(I #2)] &];
          f @@ rt]

Sqrt[5] E^(I ArcTan[2]) // N // polarForm using this version should yield the same result as in Xerxes's answer. The upshot of this method is that the output can be copied and used as executable input, thanks to Defer[].

Answer 3

You could use David Park's Presentations add-on (see http://home.comcast.net/~djmpark/DrawGraphicsPage.html):

   << Presentations`
   ComplexToPolar[3 + 4 I]
      5 ∠ ArcTan[4/3]

Numbers in ComplexPolar form can be added, multiplied, etc., then converted using PolarToComplex.