How to shorten the length of the tangent line

Question

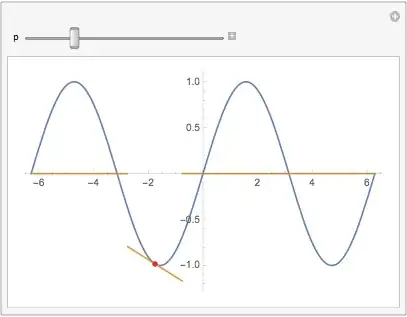
I have all the equations down to manipulate the tangent line on the graph... but the tangent line is too long, what would be the best way to shorten it?

f[x_] = Sin[x];

Plot[f[x], {x, -2 Pi, 2 Pi}]

tangent[f_, a_, x_] := f'[a] (x - a) + f[a]

Manipulate[Plot[{f[x], tangent[f, p, x]}, {x, -2 Pi, 2 Pi}, Epilog -> {Red, PointSize[.015], Point@{p, Sin[p]}}], {p, -Pi, Pi}]

Related question: https://mathematica.stackexchange.com/q/18090/3066 — m_goldberg, Sep 19 '19 at 12:00

score 3 · Answer 1 · answered Sep 19 '19 at 04:54

3

This is a kludge onto your code. I would have written the whole thing rather differently.

Manipulate[
 Plot[
  {f[x], If[Abs[p - x] < 1, 100 tangent[f, p, x], 0]},
  {x, -2 Pi, 2 Pi},
  Epilog -> {Red, PointSize[.015], Point@{p, Sin[p]}}],
 {p, -Pi, Pi}]

answered Sep 19 '19 at 04:54

David G. Stork

41,180
3
34
96

1

You could replace the 0 by Indeterminate or Undefined in the If[] statement to eliminate the line along the x axis. Is the factor of 100 a typo, perhaps? – Michael E2 Sep 19 '19 at 13:23

score 3 · Answer 2 · answered Sep 19 '19 at 12:09

You can use ConditionalExpression as in this answer linked by m_goldberg in comments:

Manipulate[
 Plot[{f[x], ConditionalExpression[tangent[f, p, x], p - .5 <= x <= p + .5]}, 
   {x, -2 Pi, 2 Pi}, 
   Epilog -> {Red, PointSize[.015], Point@{p, Sin[p]}}], {p, -Pi, Pi}]

You can replace ConditionalExpression[...] with

Piecewise[{{tangent[f, p, x],  p - .5 <= x <= p + .5}}, Undefined]

to get the same result.

How to shorten the length of the tangent line

2 Answers2

Linked