Compute of angle tangent line

Question

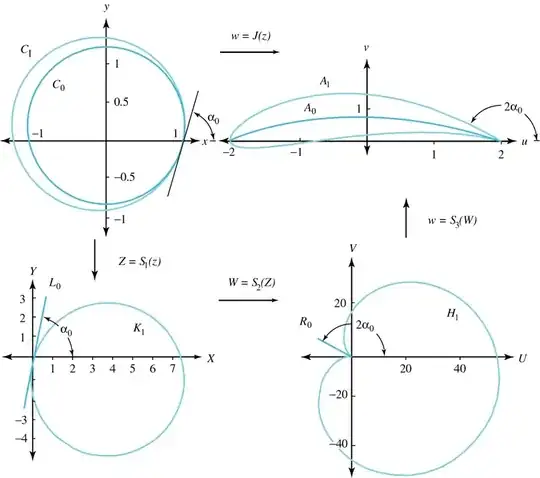
I have a problem with computing of $\alpha_{0}$ like on the figure for

joukowski[c_][{x_, y_}] := {x, y} + 1/(x^2 + y^2) {x, -y}

How to show on manipulate tangent line and change of $\alpha$ that $\alpha$ for this simulations:

Manipulate[
  Module[{radius = Max[Norm[{1, 0} - center], Norm[{1, 0} - center]], circle}, 
    circle = 1 {Cos[#], Sin[#]} + center &; 
    ParametricPlot[
      {circle[θ], joukowski[1][circle[θ]]}, {θ, 0, 2 π}, 
      PlotRange -> 2.5, 
      Epilog -> 
        {AbsolutePointSize[10], 
         Blue, Point[{1, 0}], Point[{-1, 0}], 
         Red, Circle[{-0.2, 0.2}, 0.08], 
              Circle[{-0.2, 0.2}, 0.05], 
              Circle[{-0.2, 0.2}, 0.02], 
              Line[{{-0.2, 0.1}, {-0.2, 0.3}}], 
              Line[{{-0.3, 0.2}, {-0.1, 0.2}}]}, 
      PlotStyle -> {{Thick, Blue}, {Thick, Red}}, 
      ImageSize -> {480, 480}]], 
  {{center, {0, 0}}, Locator}, 
  SaveDefinitions -> True]