0

I am trying to convolve a square wave (a diffraction grating phgrating with slits size \[CapitalLambda]) with a point spread function (PSF) to account for the finite size of the pixels.

I should get a "smoother" square wave -- indeed, this is what I get. But it always ends up being rescaled depending on the paramters of phgrating and PSF in ways I do not understand.

Definitions of PSF and phgrating:

PSF[rx_, x_, \[Gamma]_] := Exp[-(x^2/(2 rx^2))^\[Gamma]]

phgrating[x_, \[CapitalLambda]_, \[Phi]_] := \[Phi]/2 + 
  Sum[(\[Phi])*2/\[Pi] 1/(2 n - 1)*
    Sin[(\[Pi] (2 n - 1) x)/\[CapitalLambda]], {n, 1, 500}]

Function that generates discrete sets from PSF and phgrating for faster computation (psf and gr respectively):

PSFdiff[\[CapitalLambda]_, \[Phi]_, Nslits_, rx_, \[Gamma]_] := 
 Module[{x},
  gr = Table[{x, 
     phgrating[
      x, \[CapitalLambda], \[Phi]]}, {x, -Nslits \[CapitalLambda], 
     Nslits \[CapitalLambda], \[CapitalLambda]/100}];
  psf = Table[{x, PSF[rx, x, \[Gamma]]}, {x, -Nslits \[CapitalLambda],
       Nslits \[CapitalLambda], \[CapitalLambda]/100}] // Quiet;
  {gr, psf}
  ]

Example 1:

{gr, psf} = PSFdiff[1, \[Pi], 3, 0.1, 1];

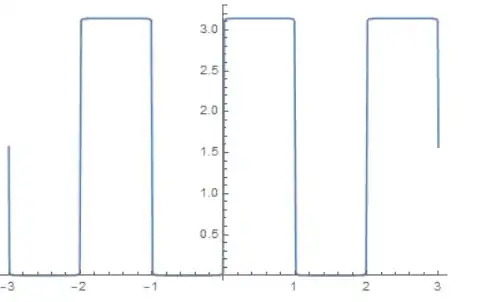
The grating, as expected, goes from 0 to \[Pi] with each "slit" size 1:

ListLinePlot[gr]

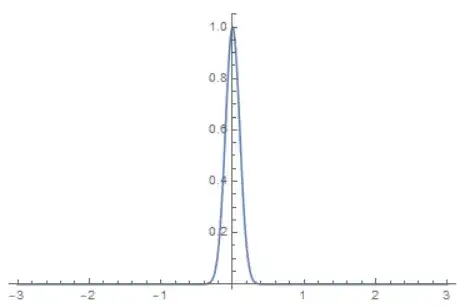
enter image description here

The point spread function also makes sense:

ListLinePlot[psf, PlotRange -> Full]

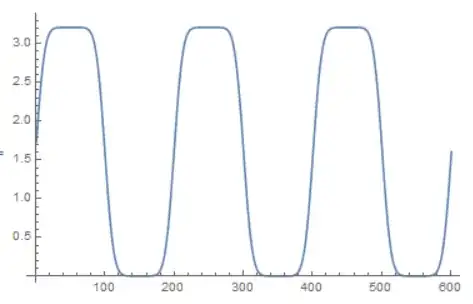
enter image description here

Now I try to compute the convolution via the convolution theorem, and I get this:

ll = InverseFourier[
    Fourier[Transpose[psf][[2]]]*Fourier[Transpose[gr][[2]]]] // Chop;
ListLinePlot[ll]

enter image description here

Apart from the fact that it is shifted with respect to the original phase grating, the scaling is fine.

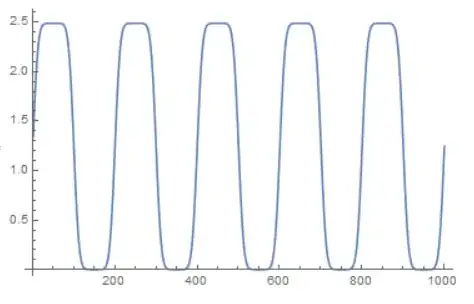
Example 2:

Same parameters as before, just chaning \[CapitalLambda] from 3 to 5:

{gr, psf} = PSFdiff[1, \[Pi], 5, 0.1, 1];

and this is the result:

enter image description here

shifted again but now also scaled!

I tried to play around with FourierParameters but did not manage to make sense of all the outcomes.

SuperCiocia
  • 1,472
  • 8
  • 15
  • When you convolve in the frequency domain should you also conjugate one of the two Fourier transforms you are multiplying? Does that make a difference? – Hugh Sep 24 '19 at 19:45
  • Maybe that explains the apparent shifting of the square wave. But not the scaling factor? – SuperCiocia Sep 24 '19 at 19:46
  • In this post I use FourierParameters ->{-1,-1}. This means that the total square in the frequency domain equals the mean square in the time domain. Do you need to get the area under the PSF equal to one? – Hugh Sep 24 '19 at 19:50
  • Hi, I use your FourierParameters convention, I normalised the kernel, and I multiply the InverseFourierTransform by the step-size between points... and now it works... – SuperCiocia Sep 25 '19 at 01:06

1 Answers1

2

You are missing two scaling factors: (I) Factor in convolution theorem; (II) Factor in Kernel.

Factor (I)

To compute the factor in a linear transform (Fourier, convolution, etc.), it is helpful to first try the delta function. In the discrete case here, it is Kronecker delta.

The default Fourier transform (FT) in Mathematica has a $1/\sqrt{n}$ factor beside the summation. After product of two FT and an inverse FT, we left factor of $1/\sqrt{n}$.

n = 10;
kd = Table[Boole[i==1],{i,n}];
fkd = InverseFourier[Fourier[kd]*Fourier[kd]];
fkd[[1]] - 1/Sqrt[n]  (* = 0 *)

Conceptually it is (FT and invFT are non-scaled Fourier transform)

$$ \frac{1}{\sqrt{n}} \textrm{invFT}\left[\frac{1}{\sqrt{n}} \textrm{FT}[a] \cdot \frac{1}{\sqrt{n}}\textrm{FT}[b] \right] = \frac{1}{\sqrt{n}} \left( \frac{1}{n} \textrm{invFT}\left[ \textrm{FT}[a] \cdot \textrm{FT}[b] \right] \right). $$

The RHS shows the factor $\frac{1}{\sqrt{n}}$ and the usual convolution theorem.

Factor (II)

Usually, one would wish the PSF do not change the signal amplitude, particularly the DC signal. So simply normalize the kernel to summation one would do it.

Result

Put these two factors together we have the correctly scaled convolution theorem:

ll = Sqrt[Length[gr]]/
    Total[Transpose[psf][[2]]] InverseFourier[
     Fourier[Transpose[psf][[2]]]*Fourier[Transpose[gr][[2]]]] // Chop;
ListLinePlot[ll]

Corrected example 2

This correspond to your example 2.

Eddy Xiao
  • 584
  • 6
  • 8