Recently I have asked the question about convolution and how to calculate it numerically.
I still misunderstand the following moment: if I have two functions defined on a grid {x,y}, so I have two arrays f[x,y] and g[x,y]. Then, I use Fourier to obtain Fourier transforms of my functions, FTf and FTg, respectively, and compute
listw=InverseFourier[FTf*FTg]
The question is following: if initial functions were defined in domain {x,y} can I assume that values of convolution $w=f*g$ are defined on the same domain? Can I just use ListPlot3D with input {x,y,w[x,y]} where x and y correspond to original grid?
Consider the example with f[x,y]=g[x,y]=Exp[-(x^2+y^2)] evaluated for x and y from [0,1] with step 0.1.
Numerical evaluation is:
center[array_] :=
RotateRight[Map[RotateRight[#, Floor[Length[array]/2]] &, array],
Floor[Length[array]/2]];
s=0.1;
a = 1.;
f[x_, y_] := Exp[-(x^2 + y^2)];
g[x_, y_] := Exp[-(x^2 + y^2)];
n = Table[x, {x, -a, a, s}] // Length;
fdata = Table[f[x, y], {x, -a, a, s}, {y, -a, a, s}];
gdata = Table[g[x, y], {x, -a, a, s}, {y, -a, a, s}];
FTf = center[Fourier[fdata]];
FTg = center[Fourier[gdata]];
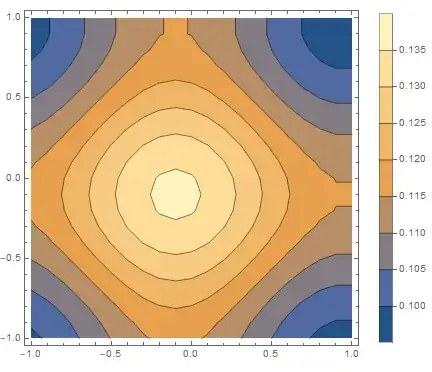
listw = Abs[1/Total@Flatten[gdata, 1]*Sqrt[n]*center[InverseFourier[FTf*FTg]]];
List density plot of listw with mentioned {x,y} values gives
Then, "exact" calculation,
FTf1 = FourierTransform[f[x, y], {x, y}, {w1, w2}];
FTf2 = FourierTransform[g[x, y], {x, y}, {w1, w2}];
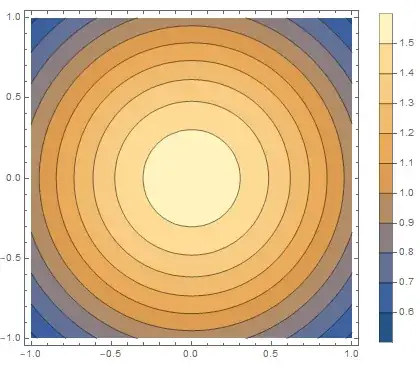
wfunction = 2*Pi*InverseFourierTransform[FTf1*FTf2, {w1, w2}, {x, y}]
gives the following density plot,
I do not understand how it happens. I try to take into account scaling factors using this question
flat = Flatten[MapIndexed[Append[#2,#1]&, listw,{2}],1]. If you need to rescale the integer coordinates back into some other domain, useMap[{Rescale[#[[1]], {xmin,xmax}],Rescale[#[[2]], {ymin,ymax}],#[[3]]}&, flat]– flinty Jun 19 '20 at 15:10listwbut I am not sure that this function is defined on the the same lattice – Artem Alexandrov Jun 19 '20 at 15:29Rescaleto{xmin,xmax}={-1,1}after the invert. Is your grid regular? – flinty Jun 19 '20 at 15:31ListCorrelate. – yarchik Jun 19 '20 at 16:19