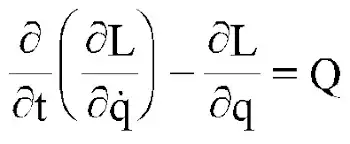Lagrangian of three-mass system with Mathematica

Question

Before proceeding to calculations in Mathematica, I would like to clarify with knowledgeable people.

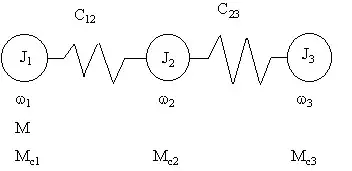
There is an ordinary linear three-mass system.

If we write its Lagrangian, we get the following equation.

where $W_k$ and $W_n$ - kinetic and potential energy.

To find the moment of rotation of the first mass, we must differentiate lagrangian first by the angle of rotation of the first mass $\phi_1$, then find the rate of change in time of the Lagrangian derivative with respect to speed $\omega_1$.

Suppose we want to find the moment of the first mass $J_1$ (we assume that on the shaft of the drive motor).

$\frac{\partial L}{\partial q} = \frac{\partial L}{\partial \phi_1} = -c_{12} (\phi_1 - \phi_2)$

$\frac{d}{dt}\frac{\partial L}{\partial \dot{q}} = \frac{d}{dt}\frac{\partial L}{\partial \omega_1} = J_1 \frac{\partial \omega_1}{\partial t}$

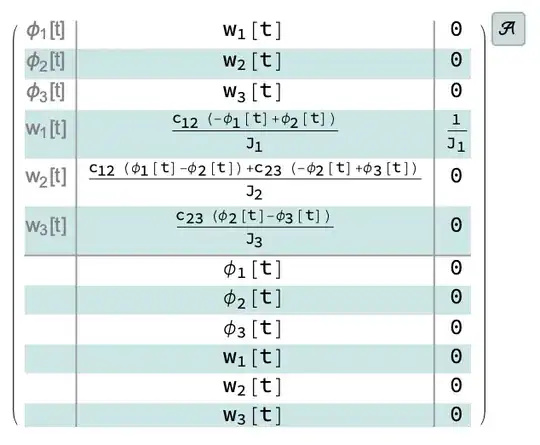
Which ultimately gives us a dynamic equation:

$M - c_{12} (\phi_1 - \phi_2) = J_1 \frac{\partial \omega_1}{\partial t}$

My questions are as follows:

Where did the masses of $J_2$ and $J_3$ go? Because we are looking for a derivative and speeds of this masses $\omega_2$ and $\omega_3$ do not explicitly depend on $\omega_1$, no matter how massive they are, they do not include into the equation of motion and do not affect the torque M.
Do I understand correctly that taking into account the influence of the moments of inertia of the remaining masses $J_2$ and $J_3$ is possible only by bringing the moments of inertia to the motor shaft $J_1$ (by correcting the coefficients of the square of the gear ration).
What tools are there in Mathematica for working with mechanical systems, equations of motion, etc.?

I am not sure if it is a Mathematica question! Usually we prefer something with some mathematica code to work with. You can construct the differential equations and we would be interested in solving them with mathematica. Meantime have a look at this link on Lagrangian dynamics with Mathematica. — Sumit, Jan 14 '20 at 08:44
I am not clear about how the rotation comes into the problem. The diagram looks like three masses connected by springs with everything in translation. Is the problem actually one of rotation and the springs are providing a torque? Are we meant to see an axis of rotation in the above problem? — Hugh, Jan 14 '20 at 13:09
I just want to calculate the driving moment of the first mass using the Lagrange equation. — dtn, Jan 14 '20 at 13:36
The problem lies in the fact that when differentiating the Lagrangian with respect to the generalized coordinate (in our case this $\omega_1$, the components of kinetic energy that are not clearly connected with the velocity of the first mass ($\omega_2$ and $\omega_3$) disappear and it turns out that the equation of motion of the first mass does not depend on the masses of the second and subsequent masses. Look at the Lagrangian and see for yourself. — dtn, Jan 14 '20 at 13:44

score 3 · Answer 1 · answered Jan 14 '20 at 11:26

3

Below is the equation of motion of the system given in OP. You need to use the variational package in Mathematica. The equation of motion is arrived at without considering the rotational inertia. And use NDsove to find the system solution.

ClearAll["Global`*"];
<< VariationalMethods`
Needs["DifferentialEquations`NDSolveProblems`"];
Needs["DifferentialEquations`NDSolveUtilities`"];
T = 0.5*m1*(D[x1[t], {t, 1}])^2 + 0.5*m2*(D[x2[t], {t, 1}])^2 + 
   0.5*m3*(D[x3[t], {t, 1}])^2;
V = 0.5*Subscript[C, 12]*(x1[t] - x2[t])^2 + 
   0.5*Subscript[C, 23]*(x2[t] - x3[t])^2;
Lg = T - V;
e1 = EulerEquations[Lg, {x1[t], x2[t], x3[t]}, {t}];
e2 = FullSimplify[e1[[1]]]
e3 = FullSimplify[e1[[2]]]
e4 = FullSimplify[e1[[3]]]

answered Jan 14 '20 at 11:26

acoustics

1,709
9
20

how adequate is the result of calculating the generalized forces? – dtn Jan 14 '20 at 11:35
And why is the second and third mass not affected by the equation of motion of the first mass? – dtn Jan 14 '20 at 11:43
1

@AndrewSol you have to do the future analysis to check whether the result is adequate or not. – acoustics Jan 14 '20 at 13:15
The problem lies in the fact that when differentiating the Lagrangian with respect to the generalized coordinate (in our case this $\omega_1$, the components of kinetic energy that are not clearly connected with the velocity of the first mass ($\omega_2$ and $\omega_3$) disappear and it turns out that the equation of motion of the first mass does not depend on the masses of the second and subsequent masses. Look at the Lagrangian and see for yourself. – dtn Jan 14 '20 at 13:45

Suba Thomas · Accepted Answer · 2020-01-15T14:33:26.370

2

First let me derive the equations of motion.

The Lagrangian:

L = Sum[1/2 Subscript[J, i] D[Subscript[\[Phi], i][t], t]^2, {i, 3}] -
   Sum[1/2 Subscript[c, 
    10 i + i + 
     1] (Subscript[\[Phi], i][t] - Subscript[\[Phi], i + 1][t])^2, {i,
     2} ]

The equations of motion:

TableForm[
 eqns = Table[
    D[D[L, Derivative[1][q][t]], t] - D[L, q[t]] == 
     Subscript[τ, q][t], 
         {q, {Subscript[ϕ, 1], Subscript[ϕ, 2], 
      Subscript[ϕ, 3]}}] /. 
       {Subscript[τ, Subscript[ϕ, 1]][t] -> M[t], 
    Subscript[τ, Subscript[ϕ, 2]][t] -> 0, 
         Subscript[τ, Subscript[ϕ, 3]][t] -> 0}]

A state-space representation:

asys=AffineStateSpaceModel[
 AffineStateSpaceModel[
  eqns, {Subscript[ϕ, 1][t], Subscript[ϕ, 2][t], 
   Subscript[ϕ, 3][t], Derivative[1][Subscript[ϕ, 1]][t], 
   Derivative[1][Subscript[ϕ, 2]][t], 
   Derivative[1][Subscript[ϕ, 3]][t]}, 
  M[t], {Subscript[ϕ, 1][t], Subscript[ϕ, 2][t], 
   Subscript[ϕ, 3][t], Derivative[1][Subscript[ϕ, 1]][t], 
   Derivative[1][Subscript[ϕ, 2]][t], 
   Derivative[1][Subscript[ϕ, 3]][t]}, 
  t], {Subscript[ϕ, 1][t], Subscript[ϕ, 2][t], 
  Subscript[ϕ, 3][t], Subscript[w, 1][t], Subscript[w, 2][t], 
  Subscript[w, 3][t]}]

I think in the first question you are asking if the input torque has any effect on the the second and third masses. From the 4th equation we can see that the input affects $w_1$. The bigger the mass the more the effort involved will be because $J_1$ is in the denominator. $w_1$ affects $\phi_1$. $\phi_1$ affects $w_2$, which affects $\phi_2$. $\phi_2$ affects $w_3$ which affects $\phi_3$. There is also some coupling in the sense that not only does $w_1$ affects $\phi_1$ but $\phi_1$ as well, etc. Also as I mentioned before the heavier the masses, the less some these influences will be.

Alternatively, you could just ask if all the positions and velocities can be adjusted using the torque on the first mass.

ControllableModelQ[%]

True

If we look a the transfer function we see that all the variables depend on all the inertia terms.

tfm = TransferFunctionModel[asys, s]

The generalized force is $M[t]$. From the last element of the transfer function which is that for $\frac{w_3(s)}{M(s)}$ we can obtain the following relationship for the generalized force.

M[s] /. Solve[Subscript[w, 3][s]/M[s] == 
    SystemsModelExtract[tfm, 1, -1][s][[1, 1]], M[s]][[1]];

InverseLaplaceTransform[% /. 
  Subscript[w, 3][s] -> LaplaceTransform[Subscript[w, 3][t], t, s], s, t]/. _[0] -> 0

Lastly, you can see examples of such systems in AffineStateSpaceModel and related documentation.

edited Jan 15 '20 at 14:33

answered Jan 14 '20 at 14:56

Suba Thomas

8,716
1
17
32

https://engineering.stackexchange.com/questions/13173/inertia-referred-to-motor-shaft – dtn Jan 14 '20 at 17:58
Imagine that the first mass is connected to the second via a gearbox with a gear ratio of $ n_1 $, and the second mass is connected to the third through a gearbox with a gear ratio of $ n_2 $. Now try to write in the Lagrangian instead of the velocities and angles of the second and third masses not $ \omega_2 $ and $ \omega_3 $ ($ \phi_2 $ and $ \phi_3 $ for angles), but $ \omega_1 / n_1 $ and $ \omega_1 / ( n_1 * n_2) $ ($ \phi_1 / n_1 $ and $ \phi_1 / (n_1 * n_2) $ for angles). Isn't this the way to go? – dtn Jan 14 '20 at 18:17
Let's say I want to find the moment needed to rotate this whole structure. By such differentiation of the Lagrangian, it turns out that the moment of the drive motor depends only on the intrinsic moment of inertia and acceleration, which, to put it mildly, is strange. – dtn Jan 14 '20 at 18:31
@AndrewSol, I think I am not understanding your confusion. I get that if you add gears the variables have to be scaled. Try SystemsModelExtract[TransferFunctionModel[affine model, s], All, 1] and you will see that $\phi_1$ depends on all the inertias. If this is not the issue, could you reformulate your question. – Suba Thomas Jan 14 '20 at 18:32
I am interested in the generalized force (moment) of the first mass. Try to manually differentiate the Lagrangian by the generalized coordinates of the first mass and you will understand me. – dtn Jan 14 '20 at 18:49
The generalized force on the first mass is $M$, which from the transfer function is $\frac{a}{b}$, where $b=c_{12} c_{23}$ and $a=c_{12} c_{23} J_1 \phi 3'(t)+c{12} c_{23} J_2 \phi 3'(t)+c{12} c_{23} J_3 \phi 3'(t)+c{23} J_1 J_2 \phi 3{}^{(3)}(t)+c{12} J_1 J_3 \phi 3{}^{(3)}(t)+c{23} J_1 J_3 \phi 3{}^{(3)}(t)+c{12} J_2 J_3 \phi _3{}^{(3)}(t)+J_1 J_2 J_3 \phi _3{}^{(5)}(t)$. – Suba Thomas Jan 14 '20 at 19:00
This formula does not follow from operations with the Lagrangian. – dtn Jan 14 '20 at 19:51
I got it from the Lagrangian. You have to consider all the equations. – Suba Thomas Jan 14 '20 at 19:53
Strange thing is that this does not involve the operation of bringing the moments of inertia to the motor shaft..6.4.Referring moment of inertia – dtn Jan 15 '20 at 04:50
@ Suba Thomas - how did you get this transfer function? – dtn Jan 15 '20 at 08:00
I showed the transfer function a couple of comments above, but then I made a typo in a subsequent comment. It should be $w_3$ and not $\phi_3$. I have updated the answer. – Suba Thomas Jan 15 '20 at 14:23
I have a question. When we get the transfer function, then we can represent it in the form of a state space. Is it possible to find some kind of expansion for matrix $A$ to separate the stiffnesses $c_{ij}$ and moments of inertia $J_i$? – dtn Jun 24 '21 at 10:52
1

I don't think that's possible. The state-space is a first-order vector matrix equation where these are not separated. The standard Lagrangian form or the Kane's formulation separates the inertia and stiffness terms. – Suba Thomas Jun 24 '21 at 15:32
Is it possible to demonstrate this in Mathematica? This separation is very useful to me, i.e. simplifies work with variable moments of inertia – dtn Jun 24 '21 at 16:24
1

vars = {Subscript[\[Phi], 1][t], Subscript[\[Phi], 2][t], Subscript[\[Phi], 3][t]}; dVars = D[vars, t]; d2Vars = D[dVars, t];
D[Subtract @@@ eqns, {d2Vars}] (* generalized mass matrix *)

D[Subtract @@@ eqns, {dVars}] (* generalized damping matrix *)

D[Subtract @@@ eqns, {vars}] (* generalized stiffness matrix *)

-Subtract @@@ eqns /. Thread[Join[vars, dVars, d2Vars] -> 0] (* generalized forces*)
– Suba Thomas Jun 24 '21 at 19:08
Is there results correct? https://ibb.co/d6qWdCG – dtn Jun 25 '21 at 06:23
1

Put each D[...](*...*) and the final -Subtract... in a new line. I was not able to convey that properly in the comment above. – Suba Thomas Jun 25 '21 at 12:53
1

I don't quite follow what you mean by 'non-stationary', but can you obtain Lagrange's equations for such non-stationary moments of inertia? – Suba Thomas Jun 27 '21 at 00:39
And how include gear ratios in Lagrangian ? – dtn Jun 27 '21 at 14:48
1

If $r$ is a gear ratio, you simply can write one angular velocity in terms of the other as $\omega _1=r \ \omega _2$ and make that substitution in the Lagrangian. It's straightforward? – Suba Thomas Jun 28 '21 at 00:13
https://mathematica.stackexchange.com/questions/250286/equations-of-motion-for-two-mass-torsional-oscillator-with-the-gear-train – dtn Jun 28 '21 at 11:49
But then it turns out that the Lagrangian depends on only one velocity? And the second generic coordinate will disappear? – dtn Jun 28 '21 at 11:50
https://mathematica.stackexchange.com/questions/250700/lagrangian-including-vector-and-matrices-operations – dtn Jul 08 '21 at 05:40
Please see the question in your free time https://math.stackexchange.com/questions/4271830/equations-of-motion-with-gear-ratios-through-the-lagrangian-with-an-unknown-tran – dtn Oct 09 '21 at 10:04

Lagrangian of three-mass system with Mathematica

2 Answers2

Linked