Equations of motion for two-mass torsional oscillator with the gear train

Question

This is my first topic and I continue work on that: Lagrangian of three-mass system with Mathematica

I found interesting problem here, and try reproduce results.

Assumption: $d_1=0$

Algorithm:

1. Write Lagrangian:

$L=W_k-W_p=\frac{J_1 \omega_1^2}{2}+\frac{J_2 (\frac{r_2}{r_1}\omega_2)^2}{2}-\frac{c_1(\phi_1-\frac{r_2}{r_1}\phi_2)^2}{2}$

where $W_k$ and $W_n$ - kinetic and potential energy.

2. Using formula:

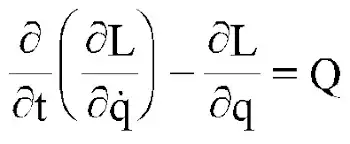
find equation of motion for coordinates:

$\frac{d}{dt}\frac{\partial L}{\partial \dot{\phi_1}}-\frac{\partial L}{\partial \phi_1}=0$

$\frac{d}{dt}\frac{\partial L}{\partial \dot{\phi_2}}-\frac{\partial L}{\partial \phi_2}=0$

I implemented all this in Mathematica:

Clear["Derivative"];
ClearAll["Global`*"];
Remove[c, J, r];
L = Sum[1/2 Subscript[J, i] D[Subscript[[Phi], i][t], t]^2, {i, 2}] -
    Sum[1/2 Subscript[c, 
      10 i + i + 
       1] (Subscript[[Phi], i][t] - 
        Subscript[[Phi], i + 1][t])^2, {i, 1}];
L = -(1/2) Subscript[c, 
    12] (Subscript[[Phi], 1][
       t] - ((Subscript[r, 2]/Subscript[r, 1]) Subscript[[Phi], 2][
         t]))^2 + 
   1/2 Subscript[J, 1] Derivative[1][Subscript[[Phi], 1]][t]^2 + 
   1/2 Subscript[J, 
    2] ((Subscript[r, 2]/Subscript[r, 1]) Derivative[1][
       Subscript[[Phi], 2]][t])^2;
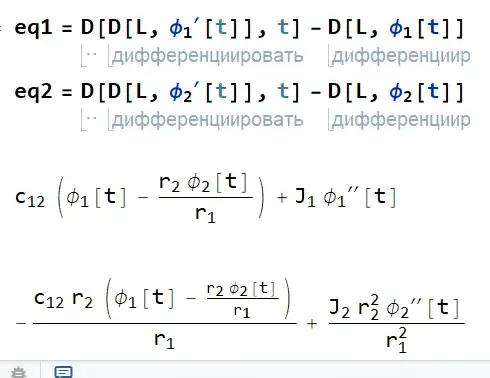
eq1 = D[D[L, Derivative[1][Subscript[[Phi], 1]][t]], t] - 
  D[L, Subscript[[Phi], 1][t]]
eq2 = D[D[L, Derivative[1][Subscript[[Phi], 2]][t]], t] - 
  D[L, Subscript[[Phi], 2][t]]

But the results didn't match the picture. Where did I go wrong?

EDIT:

There is my code for three-mass system:

Clear["Derivative"]
ClearAll["Global`*"]
Remove[c, J]
(***Gear ratios)
gr = {Subscript[n, 1], Subscript[n, 2]};
L = Sum[1/2 Subscript[J, i] D[Subscript[[Phi], i][t], t]^2, {i, 3}] -
    Sum[1/2 Subscript[c, 
      10 i + i + 
       1] (Subscript[[Phi], i][t]/gr[[i]] - 
        Subscript[[Phi], i + 1][t])^2, {i, 2}];
eq1 = D[D[L, Derivative[1][Subscript[[Phi], 1]][t]], t] - 
     D[L, Subscript[[Phi], 1][t]] == Subscript[T, 1][t] // Simplify;
eq20 = D[D[L, Derivative[1][Subscript[[Phi], 2]][t]], t] - 
     D[L, Subscript[[Phi], 2][t]] == Subscript[T, 2][t] // Simplify;
eq3 = D[D[L, Derivative[1][Subscript[[Phi], 3]][t]], t] - 
     D[L, Subscript[[Phi], 3][t]] == Subscript[T, 3][t] // Simplify;
eq2 = ApplySides[Expand[Subscript[n, 1]^2*#1] &, 
   eq20 /. Subscript[n, 1] -> 1/Subscript[n, 1]];

Answer 1

gr =.; (*Subscript[r, 2]/Subscript[r, 1]*) 
igr =.; (*Subscript[r, 1]/Subscript[r, 2]*)
twist = -gr*Subscript[ϕ, 2][t] - Subscript[ϕ, 1][t]; 

L = Sum[(1/2)*Subscript[J, i]*D[Subscript[ϕ, i][t], t]^2, {i, 2}] - 
    (1/2)*Subscript[c, 1]*twist^2; 

eq1 = D[D[L, Derivative[1][Subscript[ϕ, 1]][t]], t] - D[L, Subscript[ϕ, 1][t]] == 
      Subscript[T, 1][t] + Subscript[d, 1]*D[twist, t]//Expand
eq20 = D[D[L, Derivative[1][Subscript[ϕ, 2]][t]], t] - D[L, Subscript[ϕ, 2][t]] == 
      Subscript[T, 2][t] + Subscript[d, 1]*D[twist, t]*gr; 
eq2 = ApplySides[Expand[igr^2*#1] & , eq20 /. gr -> 1/igr]

$c_1 \text{gr} \phi _2(t)+c_1 \phi _1(t)+J_1 \phi _1''(t)=-d_1 \text{gr} \phi _2'(t)-d_1 \phi _1'(t)+T_1(t)\\c_1 \text{igr} \phi _1(t)+c_1 \phi _2(t)+\text{igr}^2 J_2 \phi _2''(t)=-d_1 \text{igr} \phi _1'(t)-d_1 \phi _2'(t)+\text{igr}^2 T_2(t)$