4

Consider the list of points

pts = {{1, 1}, {1, 2}, {2, 1}, {2, 2}}

I want to use them to define a 2x2 square mesh using VoronoiMesh, where each cell has two neighbours. Following the discussion in this question, consider the following code

mesh = VoronoiMesh[pts, ImageSize -> Medium];
conn = mesh["ConnectivityMatrix"[2, 1]];
adj = conn.Transpose[conn];
centers = PropertyValue[{mesh, 2}, MeshCellCentroid];
g = AdjacencyGraph[adj, PlotTheme -> "Scientific", 
   VertexCoordinates -> centers];
Show[mesh, g]

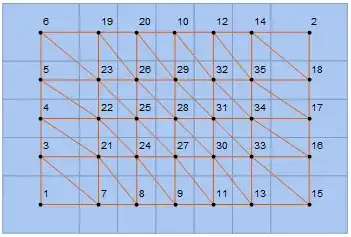
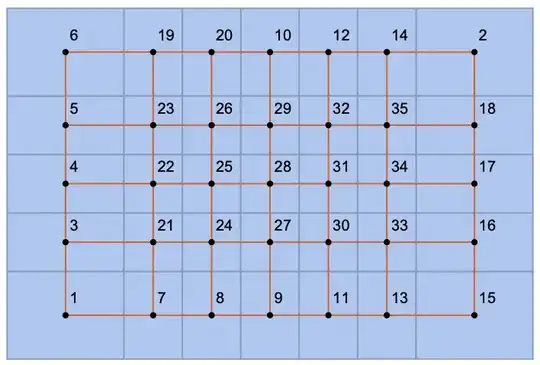
enter image description here

As one can see, unlike other meshes, this one does not seem to work exactly as I want, since the diagonal edge should not appear. Why is this happening? Any way of avoiding that edge and get

enter image description here

as one would expect from a square lattice?

Edit: As noticed in the comment section, some of the polygons seem to have sharing edges that are single points, which is enough for them to be considered neighbouring cells. This effect is unchanged with the size of the lattice. If I consider, for example, the points

pts = Flatten[Table[{i, j}, {i, 7}, {j, 5}], 1];

I get

enter image description here

Any ideas on how to solve this? Maybe omit the extra edge in a way that doesn't this or other non-square meshes. For example, considering a random VoronoiMesh, nothing seems to wrong, though it could, theoretically, go

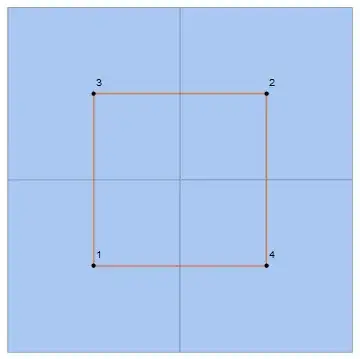
enter image description here

sam wolfe
  • 4,663
  • 7
  • 37
  • Something somewhat strange... faces 3 and 4 have 5 sides: `In[52]:= MeshCells[mesh, 2]

    Out[52]= {Polygon[{4, 1, 3, 6}], Polygon[{5, 1, 2, 9}], Polygon[{7, 3, 1, 1, 5}], Polygon[{8, 2, 1, 1, 4}]}. But notice1` is repeated twice...so structurally they share an edge, but that 'edge' is really just a point.

     – Greg Hurst Jan 15 '20 at 21:57
  • That's right. Would it be possible to delete that 1 in a reasonably natural manner? So that it wouldn't affect other possible meshes? – sam wolfe Jan 15 '20 at 22:07
  • The problem persists with bigger lattices. Please see edit section. – sam wolfe Jan 15 '20 at 22:22
  • IGraph/M handles this well. Did you try it? IGMeshCellAdjacencyGraph[mesh, 2]. You may also want to add VertexCoordinates -> Automatic – Szabolcs Jan 15 '20 at 22:26
  • No, I haven't tried yet. I think we briefly talked about this in some other post. Does IGraph/M work well with Manipulate and CDFDeploy? I'm not entirely sure how to deal with Get or Need in these type of applications. If not, I would avoid it for now, but maybe I could base it on your definition of IGMeshCellAdjacencyGraph or the adjacency matrix (which is actually what I'm interested in). – sam wolfe Jan 15 '20 at 22:29
  • Delaunay triangulation, for example, works fine in perfectly hexagonal lattices, though it seems to fail in some other cases, including the square one. Previously I was simply using DelaunayMesh[pts]["AdjacencyMatrix"]. – sam wolfe Jan 15 '20 at 22:31
  • 2
    Well, it's open-source so you can check ... It's based on Henrik's answer in the linked question. – Szabolcs Jan 16 '20 at 08:05

3 Answers3

8

We can delete the rows in our incidence matrix that correspond to these edges of length 0.

pts = Flatten[Table[{i, j}, {i, 7}, {j, 5}], 1];

mesh = VoronoiMesh[pts, ImageSize -> Medium];
conn = mesh["ConnectivityMatrix"[1, 2]];

lens = PropertyValue[{mesh, 1}, MeshCellMeasure];
$threshold = 0.;
keep = Pick[Range[MeshCellCount[mesh, 1]], UnitStep[Subtract[$threshold, lens]], 0];
conn = conn[[keep]];

adj = Transpose[conn].conn;
centers = PropertyValue[{mesh, 2}, MeshCellCentroid];
g = AdjacencyGraph[adj, PlotTheme -> "Scientific", VertexCoordinates -> centers];

Show[mesh, g]

enter image description here

Greg Hurst
  • 35,921
  • 1
  • 90
  • 136
3
L1 = 2; L2 = 2;
mesh = VoronoiMesh @ Tuples[Range /@ {L1, L2}];
centers = Rationalize @ PropertyValue[{mesh, 2}, MeshCellCentroid];

g1 = VertexReplace[GridGraph[{L2, L1}, PlotTheme -> "Scientific", 
      VertexCoordinates -> centers[[Ordering @ centers]], 
    {v_ :> Ordering[centers][[v]]}];

Show[mesh, g1]

enter image description here

For L1 = 7; L2 = 5; the same approach gives

enter image description here

kglr
  • 394,356
  • 18
  • 477
  • 896
3

You can delete the unwanted edges using EdgeDelete:

Show[mesh, EdgeDelete[g, UndirectedEdge[a_, b_] /; 
   (FreeQ[0][Chop[Differences[PropertyValue[{g, #}, VertexCoordinates] & /@ {a, b}]]])]]

enter image description here

For g generated using pts = Flatten[Table[{i, j}, {i, 7}, {j, 5}], 1]; we get

enter image description here

kglr
  • 394,356
  • 18
  • 477
  • 896