I think, I found a general and even faster way, but I haven't tested it for $1$- or $3$-dimensional MeshRegions.
The following function computes the cell-vertex-adjacency matrix A. Two $d$-dimensional cells ($d>0$) are adjacent if they share at least $d$ common points. We can find these pairs by looking for entries $\geq d$ in A.Transpose[A].
ToPack = Developer`ToPackedArray;
ClearAll[getCellCellAdjacencyList];
getCellCellAdjacencyList[R_MeshRegion, d_] :=
Module[{pts, cells, A, lens, n, m, nn},
pts = MeshCoordinates[R];
cells = ToPack[MeshCells[R, d][[All, 1]]];
lens = Length /@ cells;
n = Length[pts];
m = Length[cells];
nn = Total[lens];
A = SparseArray @@ {Automatic, {m, n}, 0, {1, {
ToPack[Join[{0}, Accumulate[lens]]],
ArrayReshape[Flatten[Sort /@ cells], {nn, 1}]
},
ConstantArray[1, nn]}};
SparseArray[
UnitStep[UpperTriangularize[A.Transpose[A], 1] - d]
]["NonzeroPositions"]
]
A special treatment is necessary for 0-dimensional cells; it's just the edges that we need.
getCellCellAdjacencyList[R_MeshRegion, 0] := ToPack[MeshCells[R, 1][[All, 1]]]
Here are some examples:
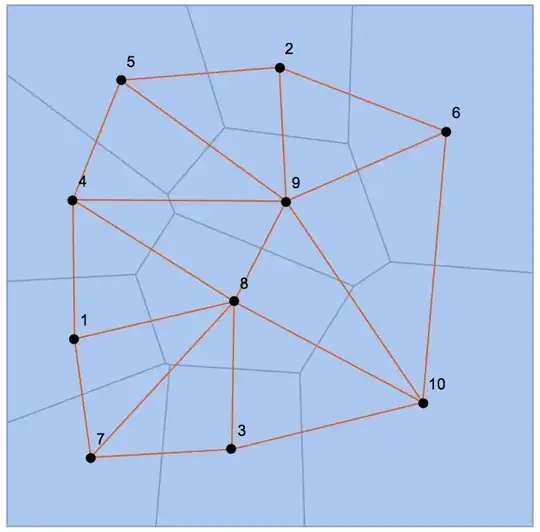
SeedRandom[123]
pts = RandomReal[1, {10, 2}];
R = VoronoiMesh[pts];
GraphicsGrid[Table[
{VoronoiMesh[pts, MeshCellLabel -> {d -> "Index"}],
Graph[getCellCellAdjacencyList[R, d], VertexLabels -> "Name"]
}, {d, 0, 2}], ImageSize -> Large]

And some timings for comparison:
SeedRandom[123]
pts = RandomReal[1, {10000, 2}];
R = VoronoiMesh[pts]; // RepeatedTiming
getCellCellAdjacencyList[R, 0]; // RepeatedTiming
getCellCellAdjacencyList[R, 1]; // RepeatedTiming
getCellCellAdjacencyList[R, 2]; // RepeatedTiming
{0.636, Null}
{0.015, Null}
{0.031, Null}
{0.041, Null}
Edit
It's now rather straight-forward to write methods for the various adjacency matrices, lists, and graphs, even for cells of different dimensions (see below).
Edit 2
As Chip Hurst pointed out, the adjacency matrix of a MeshRegion R for distinct dimensions d1, d2 can be found as pattern SparseArray under R["ConnectivityMatrix"[d1,d2]]. (Its "RowPointers" and "ColumnIndices" must have been computed immediately when the MeshRegion was built.)
Many applications of adjacency matrices, in particular in finite elements, need 1 instead of Pattern as nonzero entries. Even computing vertex rings in a graph by using MatrixPowers of the adjacency matrix is considerably faster with (real) numeric matrices. A remedy could be the function SparseArrayFromPatternArray below. As Chip Hurst has pointed out, we can turn a pattern array into a numerical one with Unitize. I updated my old code to utilize this observation, leading to a tremendous performance boost. Somewhat surprisingly, even the old implementation of CellAdjacencyMatrix[R, 1, 2] tends to be faster than R["ConnectivityMatrix"[1,2]], so that I decided to use the new approach only for the case when either d1 or d2 is equal to 0.
CellAdjacencyMatrix[R_MeshRegion, d_, 0] := If[MeshCellCount[R, d] > 0,
Unitize[R["ConnectivityMatrix"[d, 0]]],
{}
];
CellAdjacencyMatrix[R_MeshRegion, 0, d_] := If[MeshCellCount[R, d] > 0,
Unitize[R["ConnectivityMatrix"[0, d]]],
{}
];
CellAdjacencyMatrix[R_MeshRegion, 0, 0] :=
If[MeshCellCount[R, 1] > 0,
With[{A = CellAdjacencyMatrix[R, 0, 1]},
With[{B = A.Transpose[A]},
SparseArray[B - DiagonalMatrix[Diagonal[B]]]
]
],
{}
];
CellAdjacencyMatrix[R_MeshRegion, d1_, d2_] :=
If[(MeshCellCount[R, d1] > 0) && (MeshCellCount[R, d2] > 0),
With[{B = CellAdjacencyMatrix[R, d1, 0].CellAdjacencyMatrix[R, 0, d2]},
SparseArray[
If[d1 == d2,
UnitStep[B - DiagonalMatrix[Diagonal[B]] - d1],
UnitStep[B - (Min[d1, d2] + 1)]
]
]
],
{}
];
CellAdjacencyLists[R_MeshRegion, d1_, d2_] :=
If[(MeshCellCount[R, d1] > 0) && (MeshCellCount[R, d2] > 0),
Module[{i1, i2, data},
data = If[d1 == d2,
UpperTriangularize[CellAdjacencyMatrix[R, d1, d2], 1]["NonzeroPositions"],
CellAdjacencyMatrix[R, d1, d2]["NonzeroPositions"]
];
If[Length[data] > 0,
{i1, i2} = Transpose[data];
Transpose[
{
Transpose[{ConstantArray[d1, {Length[i1]}], i1}],
Transpose[{ConstantArray[d2, {Length[i2]}], i2}]
}
],
{}
]
],
{}
];
CellAdjacencyGraph[R_MeshRegion, d1_, d2_] := Graph[
Join[MeshCellIndex[R, d1], MeshCellIndex[R, d2]],
UndirectedEdge @@@ CellAdjacencyLists[R, d1, d2],
VertexLabels -> "Name"
];
Note that CellAdjacencyLists and CellAdjacencyGraph use labels that are compatible with those obtained from MeshCellIndex.
Applied to Szabolcs's example MeshRegion, theses graphs look as follows:
GraphicsGrid[
Table[CellAdjacencyGraph[R, d1, d2], {d1, 0, 2}, {d2, 0, 2}],
ImageSize -> Full]
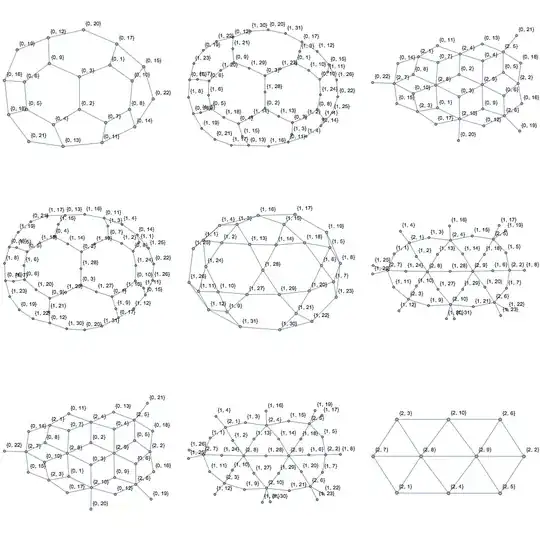
As for comparing the performance of these new implementations to getCellCellAdjacencyList:
{
getCellCellAdjacencyList[R, 0]; // RepeatedTiming // First,
getCellCellAdjacencyList[R, 1]; // RepeatedTiming // First,
getCellCellAdjacencyList[R, 2]; // RepeatedTiming // First
}
{
CellAdjacencyLists[R, 0, 0]; // RepeatedTiming // First,
CellAdjacencyLists[R, 1, 1]; // RepeatedTiming // First,
CellAdjacencyLists[R, 2, 2]; // RepeatedTiming // First
}
{0.015, 0.030, 0.037}
{0.0068, 0.011, 0.0066}









DelaunayMeshandMeshPrimitives? As inpi = PositionIndex[MeshPrimitives[DelaunayMesh[pts], 0][[;; , 1]]][[;; , 1]],Graph[Values[pi], MeshPrimitives[DelaunayMesh[pts], 1][[;; , 1]] /. pi, VertexLabels -> "Name"]. – aardvark2012 Nov 22 '17 at 10:02MeshConnectivityGraphwas later introduced in version 12.1 (2020). – userrandrand Dec 07 '22 at 19:34