The ordering problem of multivariate polynomials

Question

This is the result of Taylor expansion of a binary function

F[k_] := Sum[Binomial[k, r]*Δx^r*Δy^(k - r)*   Derivative[r, k - r][f][x0, y0], {r, 0, k}]
f[x_, y_] := x^2*y^2
Expand[Sum[F[i]/i!, {i, 0, 3}]]

$$F[\text{k$\_$}]\text{:=}\sum _{r=0}^k \text{$\Delta $x}^r \binom{k}{r} \text{$\Delta $y}^{k-r} f^{(r,k-r)}[\text{x0},\text{y0}]$$ $$f[\text{x$\_$},\text{y$\_$}]\text{:=}x^2 y^2$$ $$\text{Expand}\left[\sum _{i=0}^3 \frac{F[i]}{i!}\right]$$ The output is not ordered by the sum of the powers of $\Delta x$ and $\Delta y$ 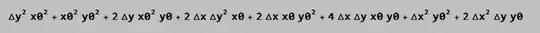But I want to sort this polynomials by power order of $\Delta x$ and $\Delta y$ like this: 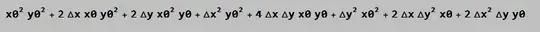How can I do this with functions like Collect or Simplify?

Is this related https://mathematica.stackexchange.com/questions/30216/how-can-i-reorder-the-factors-in-the-terms-of-a-polynomial? — , Jan 29 '20 at 00:46
@J.M. Yes, I don't want the sorting of the results to be broken by the unordered properties of the Plus function and I want to arrange the results as required. — A little mouse on the pampas, Jan 29 '20 at 00:51
@PleaseCorrectGrammarMistakes Do you want this for the output or you just want to read the resulting prefactors easily? — , Jan 29 '20 at 01:29
@A_user_with_NoName I want to read the resulting prefactors easily.I want to write a custom function to sort the output results according to the above requirements. — A little mouse on the pampas, Jan 29 '20 at 01:38
@PleaseCorrectGrammarMistakes in order for you to be able to read the prefactors easily, I suggest that you use CoefficientlList. If you are interested in reading just one prefactor quickly, then you can use Coefficient. For the custom function, I have not been able to bring it in the form that you want. The link that I posted gives similar -ish result — , Jan 29 '20 at 01:47

score 1 · Accepted Answer · answered Jan 29 '20 at 03:37

1

orderedForm[poly_, var_List] := 
  HoldForm[+##] & @@ 
   MonomialList[poly, 
     var][[Ordering[-Total[#] & @@@ CoefficientRules[poly, var], All, 
      GreaterEqual]]];
orderedForm[
 Expand[Sum[
   F[i]/i!, {i, 0, 3}]], {Δx, Δy}]

answered Jan 29 '20 at 03:37

A little mouse on the pampas

5,760
2
13
40

score 1 · Answer 2 · answered Jan 29 '20 at 05:14

Interestingly, Wolfram Cloud seems to give an almost-desired answer, clearly indicating use of a differing subroutine. Posting this an an answer as it is too much for a comment:

F[k_] := Sum[Binomial[k, r]*\[CapitalDelta]x^r*\[CapitalDelta]y^(k - r)*   Derivative[r, k - r][f][x0, y0], {r, 0, k}]
f[x_, y_] := x^2*y^2
Expand[Sum[F[i]/i!, {i, 0, 3}]]

Gives

x0^2*y0^2 + 2*x0*y0^2*\[CapitalDelta]x + y0^2*\[CapitalDelta]x^2 + 2*x0^2*y0*\[CapitalDelta]y + 4*x0*y0*\[CapitalDelta]x*\[CapitalDelta]y + 2*y0*\[CapitalDelta]x^2*\[CapitalDelta]y + x0^2*\[CapitalDelta]y^2 + 2*x0*\[CapitalDelta]x*\[CapitalDelta]y^2

While close, this does not satisfy the OP’s requirements, although it does provide impetus for further investigation of the dependence of the polynomial ordering displayed.

The ordering problem of multivariate polynomials

2 Answers2

Linked