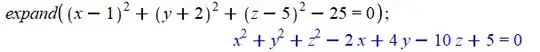With Maple, I tried
expand((x - 1)^2 + (y + 2)^2 + (z - 5)^2 - 25 = 0);
and got
With Mathematica, I tried
Expand[(x - 1)^2 + (y + 2)^2 + (z - 5)^2 - 25 == 0]
I got
5 - 2 x + x^2 + 4 y + y^2 - 10 z + z^2 == 0
How can I get the result like result of Maple?