Using Michael E2's answer, I performed a manual arclength parameterisation by solving the differential equation (or: finding the inverse of a function whose derivative is known).
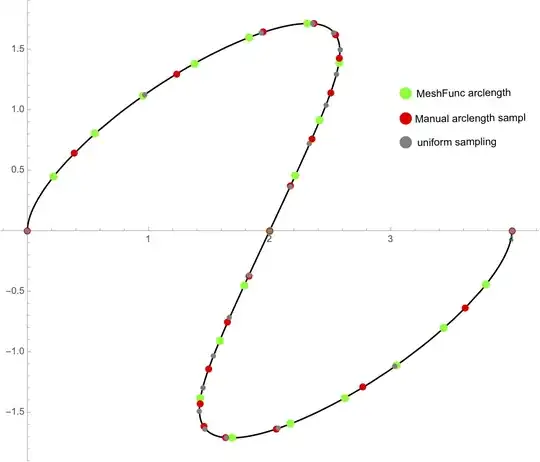
I compared the results with the built-in arclength mesh-sampling. Unexpectedly, they are not the same (see green and red points on plot).
Using the built-in function is no solution to this problem, because I need this method for some other sampling based on specific parameterisations (other than arclength).
Here's the code:
ptsp = {{0, 0}, {0, 2}, {3, 2}, {1, -2}, {4, -2}, {4, 0}};
g = BSplineFunction[ptsp, SplineWeights -> {1, 1, 15, 15, 1, 1}, SplineDegree -> 3];
ClearAll[s, t];
dg[t_?NumericQ] := If[t - 1. <= 0, g'[t], g'[1]];
tfn = NDSolveValue[{t'[s] == 1/Norm[dg[t[s]]], t[0] == 0,
WhenEvent[t[s] == 1, "StopIntegration"]},
t, {s, 0, 1 + NIntegrate[Norm[g'[t]], {t, 0, 1}]}];
ParametricPlot[g[t], {t, 0, 1},
MeshFunctions -> {"ArcLength"}, Mesh -> {20-1},
MeshStyle -> {PointSize[0.015], Green},
PlotStyle -> {Black}
Epilog -> {
PointSize[0.013], Red,
Point[g /@
tfn[Rescale[Range[0, 1, 1/20], {0, 1}, First@tfn["Domain"]]]],
PointSize[0.01], Gray, Point[g /@ Range[0, 1, 1/20]]
}
]
I also tried other methods, like this answer, which gave the same wrong result.
Does anyone have an idea why this happens for this specific B-Spline?



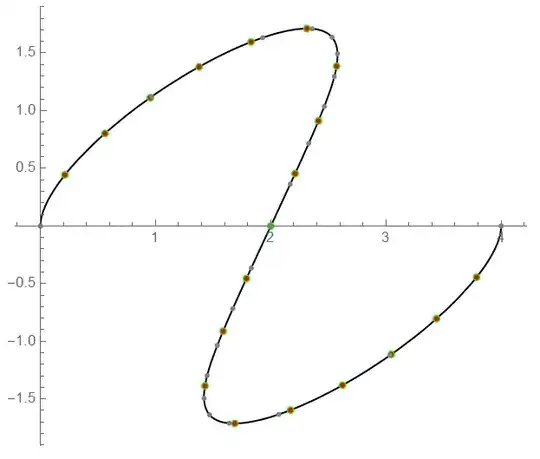
Mesh -> {20}, the points overlap perfectly (With[{n = 20}, tvals = …]also works of course). I would be pretty surprised ifMeshFunctions->"ArcLength"didn't work only for some specific functions (assuming that it performs the relevant computations on the numeric result it got from plotting the function, and doesn't use some analytic method) – Lukas Lang Feb 04 '20 at 14:14Mesh -> {20}everything's good. (LL you won for 10 seconds!) – johk95 Feb 04 '20 at 14:14