Coordinates of spline plot using ArcLength mesh function

Question

The following code produces a 3D spline with equidistant interpolation points:

Needs["Splines`"];
f = SplineFit[{{0, 0, 3}, {2, 0, 3}, {2, 2, 1}, {0, 1, 0}}, Cubic];
plot = ParametricPlot3D[f[t], {t, 0, 3}, 
  MeshFunctions -> {"ArcLength"}, Mesh -> {15}, 
  MeshStyle -> {PointSize[0.02], Red}]

How do I get the actual coordinates (list of points) of the red points? (they must be equidistant as in the plot).

Does this answer your question: Generating evenly spaced points on a curve? Also: How to get a uniformly distributed list of points from a B-spline function and Manual ArcLength sampling on spline differs ... — Domen, Apr 03 '23 at 18:34
Not really. Two cases are 2D, and 3D does not work. One case does not return coordinates. — Jaka Belec, Apr 04 '23 at 08:25

score 4 · Answer 1 · answered Apr 03 '23 at 18:44

From your plot you can extract the points. However, the points are given as indices of a list of coordinates. To get these indices:

indices = Cases[(plot // FullForm ) , Point[x_] -> x, Infinity][[1]];

Next we need to extract the list of coordinates:

coord = Cases[plot, GraphicsComplex[x_, _] -> x, Infinity][[1]];

From this list we only need to coordinates indicated by "indices:"

coord = coord[[indices]];

To test if everything works, we may plot large opaque green points over the original plot:

Show[Graphics3D[{Opacity[0.3], Green, PointSize[0.05], 
   Point[coord]}], plot]

Bob Hanlon · Accepted Answer · 2023-04-04T15:14:57.033

4

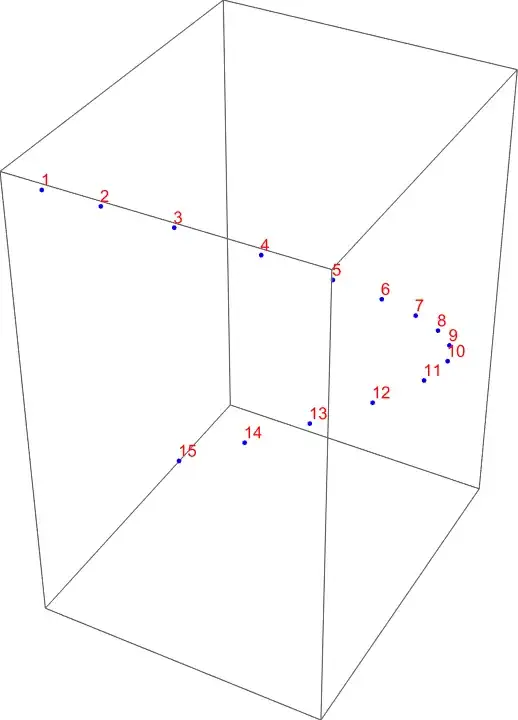
Clear["Global`*"]

Needs["Splines`"];

f = SplineFit[{{0, 0, 3}, {2, 0, 3}, {2, 2, 1}, {0, 1, 0}}, Cubic];

plot = ParametricPlot3D[f[t], {t, 0, 3}, MeshFunctions -> {"ArcLength"}, 
  Mesh -> {15}, MeshStyle -> {PointSize[0.02], Red},
  WorkingPrecision -> 15]

The red dots are located at

pts = Cases[plot // Normal, Point[pt_] :> pt, Infinity];
Length@pts
(* 15 *)

The red dots are ordered as

orderedPts = Rest@pts[[FindCurvePath[pts][[1]]]];

EDIT: Or more robustly,

orderedPts = Rest@pts[[FindShortestTour[pts][[2]]]]

They are approximately equally spaced (note that the curve length between points is not the same as the EucldeanDistance between them)

dist = EuclideanDistance @@@ Partition[orderedPts, 2, 1]
(* {0.483212, 0.482984, 0.481793, 0.477275, 0.478571, 0.482301, 0.482944, 

0.483029, 0.482915, 0.482403, 0.47809, 0.474605, 0.481376, 0.482977} *)
{Mean[dist], StandardDeviation[dist]}
(* {0.481034, 0.00274354} *)

edited Apr 04 '23 at 15:14

answered Apr 03 '23 at 18:48

Bob Hanlon

157,611
7
77
198

Thanks! I do not need exactly equal spacing, this is perfect. – Jaka Belec Apr 04 '23 at 08:03
The ordering does not quite work, e.g. for points {{-5, -2.2, 0.7}, {5, -4.5, 10}, {6.7, -9.5, 5}, {-2, -0.5, -1.5}} – Jaka Belec Apr 04 '23 at 09:17
For the ordering use orderedPts = Rest@pts[[FindShortestTour[pts][[2]]]]; – Bob Hanlon Apr 04 '23 at 15:00

cvgmt · Answer 3 · 2023-04-04T03:48:41.180

Since MaxRecursion will automatic add extra points to make the curve smooth, we need to set

MaxRecursion->0

to prevent such feature, keep the order of meshs.(to make the curve smooth, now we have to set PlotPoints -> 100.)

Clear[plot0]; 
Needs["Splines`"];
f = SplineFit[{{0, 0, 3}, {2, 0, 3}, {2, 2, 1}, {0, 1, 0}}, Cubic];
plot0 = 
 ParametricPlot3D[f[t], {t, 0, 3}, MeshFunctions -> {"ArcLength"}, 
  Mesh -> {15}, MeshStyle -> {PointSize[0.02], Red}, 
  MaxRecursion -> 0, PlotPoints -> 100];
meshs = Cases[Normal@plot0, Point[pts_] :> pts, -1];
Graphics3D[{MapIndexed[{Red, Text[First@#2, #1, {-1, -1}], Blue, 
     Point[#1]} &, meshs]}]

Coordinates of spline plot using ArcLength mesh function

3 Answers3